
Сроки действия доменов и SSL-сертификатов Н А Ш И Х сайтов заканчиваются. Д Л Я п о м о щ и в их П Р О Д Л Е Н И И СКАЧИВАЙТЕ приложения в российском магазине приложений




И явился ему во сне ДЖИНН и сказал: "Вот тебе 100000 динаров! Если будешь отдавать каждую ночь такую часть этих динаров, чтобы она была больше, чем часть предыдущей но- чи, а на последнюю ночь полной луны ты отдашь всю сумму - эти динары станут твоими." Проснулся бедняк - и сделал Э Т О. Из неопубликованных сказок "Тысяча и одна ночь".
METHODS of the NUMBER
DECOMPOSITION.
МЕТОДЫ РАСЧЁТА ДЕКОМПОЗИЦИИ
ЧИСЛА.
В А Ш МЕТОД - ЭТО ЛЕГКО!
ДЕКОМПОЗИЦИЯ
произвольного
вещественного
числа
D.
НАПРИМЕР:
ИЛИ
ИЛИ
РАЗЛОЖЕНИЕ
исходного числа
D
на
эквивалентную
по величине
сумму ряда "составных"
i-х
расчётных чисел
di,
определённых методами
декомпозиции числа.
ИЛИ
ТОЖДЕСТВО
исходного числа
D
и
суммы ряда
его
(числа)
декомпозиции.
ИЛИ
ПРЕДСТАВЛЕНИЕ
числа
D
в виде
тождественной
суммы ряда
n
наперёд заданного
конечного количества
i-х
расчётных
di
числовых слагаемых .
ПРИКЛАДНЫЕ
"МЕТОДЫ..."
высокоточных расчётов
членов ряда
di
декомпозиции числа.
* * *
РАЗЛОЖЕНИЮ
произвольного числа
D
на
n
расчётных
di
сомножителей
(многочленное произведение);
* * *
ДЕКОМПОЗИЦИЯ
НУЛЯ
D = 0.
* * *
ЗАДАЧЕ
о
подарках -
оптимальная покупка!;
* * *
ИНТЕРПРЕТАТОРУ
скоростного режима
при
старте автомобиля;
* * *
РАЗДЕЛЕНИЮ
жёсткого диска
на
разделы/подразделы;
* * *
ИНТЕРПРЕТАЦИИ
законов сохранения
физических сущностей
природы;
* * *
РАЗЛОЖЕНИЮ
натуральных чисел
в
конечные
числовые ряды;
* * *
РАЗЛОЖЕНИЮ
1
в
КОНЕЧНЫЙ
единичный ряд
(сумма ряда равна
единице);
* * *
СУММИРОВАНИЮ
вероятностей событий
(проверка);
* * *
МОДЕЛИРОВАНИЮ
систем
электрических зарядов
(школьная программа);
* * *
ОПРЕДЕЛЕНИЮ
оптических сил
системы
n
тонких линз;
* * *
ПОРТАТИВНОЙ ГЕНЕРАЦИИ
паролей
и
ключей
систем безопасности;
* * *
ШИФРОВАНИЮ
боевых
координат;
* * *
РАСЧЁТУ
"магазина"
сопротивлений,
напряжений, ёмкостей
и
индуктивностей
при
последовательном
и
параллельном
соединении проводников
электрических сетей;
* * *
ПЛАНИРОВКЕ
квадратных метров
при
"разбивке"
земельного участка
или
жилой площади
будущего дома;
* * *
РЕШЕНИЮ
уравнения
регрессии
с
n
неизвестными;
* * *
РЕШЕНИЮ
однородного
алгебраического уравнения
с
n
неизвестными;
* * *
МОДЕЛИРОВАНИЮ
векторных полей
многомерного векторного пространства;
* * *
РАСЧЁТУ
погашения
суммы
кредита / ипотеки;
* * *
ПРИЛОЖЕНИЮ
к а л
ь к у л я т о р а
графиков
платежей;
* * *
ФОРМИРОВАНИЮ
проекта бюджета
малого предприятия;
контролю расхода
статей бюджета;
* * *
РАЗРАБОТКЕ
единичных
передаточных функций
декомпозиции числа;
* * *
РУЧНОМУ РАСЧЁТУ
декомпозиции
семейного бюджета;
* * *
ДЕКОМПОЗИЦИИ
числа
PI = 3,1415926
в приложениях
геометрии
и
физики;
* * *
ОПРЕДЕЛЕНИЮ
общего
передаточного отношения
в
многоступенчатой передаче
зубчатого механизма;
* * *
ПЕРЕСЧЁТУ
декомпозиции
числа произведением
от
декомпозиции суммой;
* * *
ИЗМЕНЕНИЮ
декомпозиции числа
во
времени;
* * *
* * *
ПРИМЕНЕНИЮ
алгоритма
расчёта
приложения

к
решению
типовых задач
экономики;
* * *
РАСЧЁТУ
И
ВОСПРОИЗВЕДЕНИЮ
эпюр
и
графиков
скоростей, импульсов,
электрических сигналов
в учебных целях
и
теоретических исследованиях.

МНОГОКРАТНЫЕ ВАРИАНТЫ РАСЧЁТОВ ПО КНОПКЕБЕЗ ПЕРЕЗАГРУЗКИ СТРАНИЦЫ.
ОСНОВНОЕ СОДЕРЖАНИЕ: --------------------
Автором сайта открыт уни-
версальный алгоритм тождест-
венного представления произ-
вольного числа D в виде ко-
нечной суммы ряда заданного
числа (количества) n положи-
тельных расчётных слагаемых
("составных" чисел) di -
Д Е К О М П О З И Ц И Я
Ч И С Л А.
Модель "Метода..." декомпо-
зиции формирует строгий закон
изменения величин расчётных
слагаемых di в составе суммы
ряда разложения исходного числа
D в зависимости от их поряд-
кового номера i , а также обще-
го числа (количества) слага-
емых n .
При этом само значение сум-
мы ряда декомпозиции
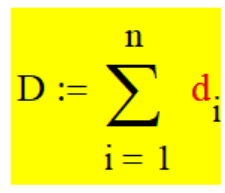
НЕ ИЗМЕНЯЕТСЯ
и сохраняется равной по вели-
чине заданному исходному числу
D ,
подлежащему декомпозиции.
Представлены три основных
"стандартных" "Метода..." рас-
чёта di - членов ряда деком-
позиции числа D .
Практическая реализация каж-
дого была проверена на тестовых
расчётах в системе Mathcad в
широком диапазоне изменения пе-
ременных декомпозиции числа -
D , di , n , i .
Результаты этих расчётов в
виде рубрик "Занимательные
шпаргалки" Mathcad, содержащие
познавательные рисунки-таблицы
декомпозиции первых 10 нату-
ральных чисел, а также расчёт-
ные графики членов ряда суммы
декомпозиции ЭТИХ чисел,
предшествуют каждому соответ-
ствующему "Методу..." и указаны
в содержании сайта.
Кроме того, для возможности
сопоставления и анализа резуль-
татов расчётов, в каждом "Мето-
де..." приведен график декомпо-
зиции условного МРОТ в сумме
10842,75 руб. при раскладе его
на 365 дней в году.
Аналогичный высокоточный рас-
чёт декомпозиции в виде теста
может быть выполнен НА САЙТЕ
любым из рассмотренных "Мето-
дов..." - величина МРОТ от этого
Н Е И З М Е Н Я Е Т С Я !
В разделах сайта, предшест-
вующих описанию переменных
"Метода...", показаны фрагменты
расчётов данного "Метода...".
В конце расчётного блока
каждого "Метода..." приводится
результат выполнения численной
"Проверки", в которой контроли-
руется равенство исходного чис-
ла D и ЕГО итоговой суммы
декомпозиции sum(i = n) , кото-
рая "набирается" из значений
"текущих" сумм sumi на каждом
i шаге (итерации) декомпози-
ции числа.
После выполнения расчётов
становятся доступными данные
по ДИАПАЗОНУ ВЕЛИЧИН СЛАГАЕМЫХ
в составе суммы декомпозиции
числа:
- максимальное значение
слагаемого суммы деком-
позиции числа;
- среднее значение
слагаемого суммы деком-
позиции числа (D/n) ;
- минимальное значение
слагаемого суммы деком-
позиции числа.
КОРРЕКТНЫЙ
ввод исходных (начальных) данных
расчёта:
- исходное число D
- вещественное/целое (поло-
жительное/отрицательное)
число;
- число (количество) слагаемых
n
- целое/положительное число.
При некорректном вводе исход-
ных данных результаты расчетов
всех "Методов..." приведены
к
1 .
Этим свойством можно восполь-
зоваться при расчётах декомпози-
ции числа
D = 1 ,
заполняя только окно ввода
требуемого количества слагаемых
n .
Окно ввода исходного числа
D
при этом остаётся незаполненным.
Такой же приём ввода исходных
данных удобен при расчётах чисел,
кратных 10 , когда
после декомпозиции 1
в результатах окончательных рас-
чётов запятая ,
переносится "вручную" на число
значащих "нулей" исход-
ного числа.
Графическая часть расчетов
по "Методам №1, №2, №3..."
в настоящем сайте представле-
на, в частности, короткой
черно-белой анимацией в конце
раздела
Видео-отчёт.
Как бедняк отдавал ДЖИННУ
100000 динаров.
Но с ней можно подробно ознако-
миться на сайте
ПОГАШЕНИЕ СУММЫ
КРЕДИТА/ИПОТЕКИ,
где рассматривается вопрос
"Декомпозиции суммы кредита
по ипотеке"
и методы "Метод №1","Метод №2",
"Метод №3" совпадают со "стандарт-
ными" "Методами №1, №2, №3..."
настоящего сайта.
При этом, высокоточные рас-
чёты ипотечных платежей сопро-
вождаются автоматическим постро-
ением графиков требуемых плате-
жей di при погашении кредитной
суммы из расчётов соответству-
ющего "Метода...".
Там же расширен модельный ряд
расчетных методов декомпозиции
числа в терминах "декомпозиции
суммы кредита" - дополнительно
представлены расчётные "Методы.."
с расширением
"mirror" ("зеркало") ,
выполняющие декомпозицию числа
B = D "Методов..." в "обратном"
порядке.
Графики расчетов этих "Ме-
тодов..- mirror" расположены
зеркально по отношению к гра-
фикам "стандартных" "Методов..".
При этом все основные свой-
ства декомпозиции числа перво-
начального "стандартного"
"Метода.." - СОХРАНЯЮТСЯ.
В "ПРИЛОЖЕНИИ САЙТА"
ПРИЛОЖЕНИЕ САЙТА.
приведены некоторые задачи, по-
добранные автором, которые до-
полнительно могут быть решены
на базе "Методов..."
ДЕКОМПОЗИЦИИ ЧИСЛА.
ДЕКОМПОЗИЦИЯ предполагает тождественное разложение не- которого исходного числа D на сумму ряда наперёд заданного конечного числа (количества) n неповторяющихся по величине расчётных положительных сла- гаемых di - "составных" чисел суммы декомпозиции.При этом обратное суммиро- вание этих расчитанных слага- емых di должно приводить по величине к первоначальному ис- ходному числу D.
Тем самым, как бы, требуется выполнение своего рода закона сохранения "численной массы" числа до и после его деком- позиции. Сами же величины рас- чётных слагаемых di по опреде- лённому закону группируются относительно своего среднего значения D/n . Вид и характер зависимости "составных" чисел di от поряд- кового № i в составе суммы декомпозиции числа D определя- ются как установленным коли- чеством слагаемых n , так и моделью расчётного "Метода..." декомпозиции. Ниже приведен краткий мате- матический блок описания деком- позиции ("разложения") числа на сумму конечного числа "сос- тавных" слагаемых.
Cхему разложения числа на слагаемые можно представить в следующем виде: D тождественно равно d1 + d2 + d3 +..+ di +..+ dn (*), где D - исходное число, подлежащее декомпозиции; di - i-е слагаемое в составе суммы ряда разложения (*); dn - n-е слагаемое в составе суммы ряда разложения (*); i - порядковый номер итерации разложения; n - общее число итераций разложения (интервал декомпозиции). При этом вариантов и мето- дов декомпозиции одного и того же числа D (не считая переста- новок слагаемых в расчётной сумме декомпозиции (*)) теорети- чески - БЕСКОНЕЧНО .
Алгоритм декомпозиции был
протестирован в системе Math-
cad и показал абсолютную точ-
ность разложения натуральных
и вещественных чисел в части
равенства исходного числа и
его суммы декомпозиции.
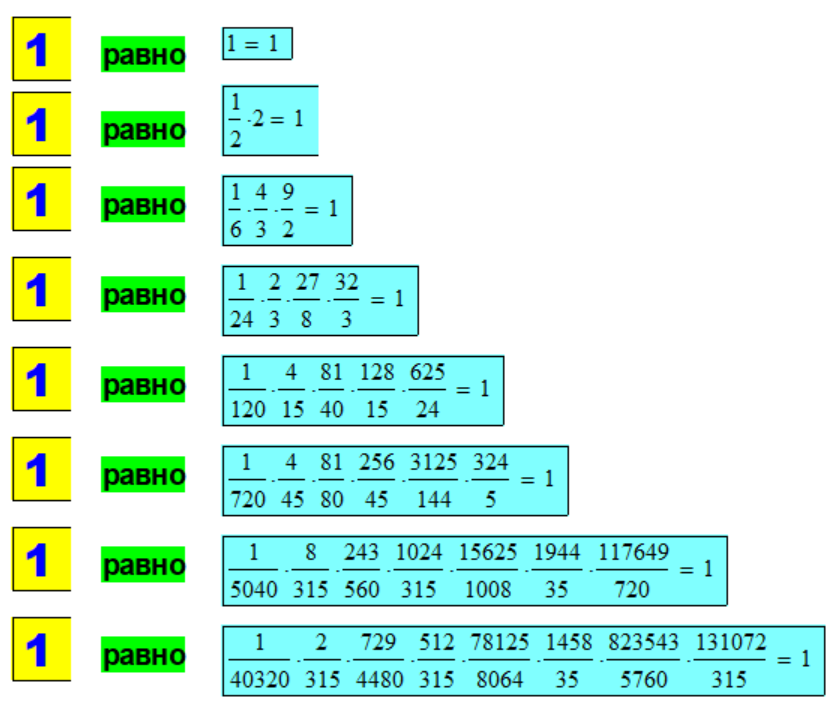
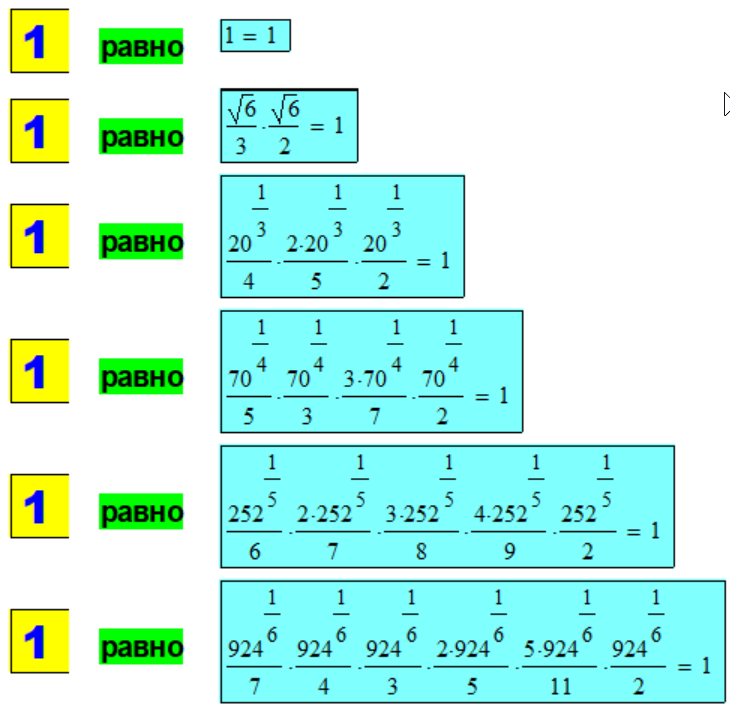
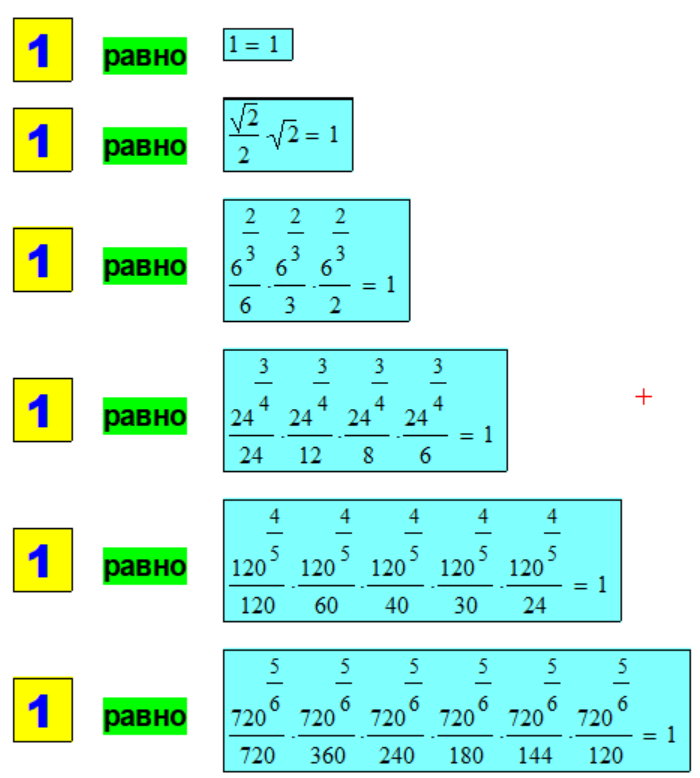
В "шапке" сайта расположен
рекламный пример декомпозиции
числа "1" в "наглядном" гра-
фическом представлении для ин-
тервалов n = 1, 2, 3, 4, 5,
6, 7, 8, 9 и 10 .
Так же с результатами те-
стирования с возможностью их
"ручной" проверки можно под-
робно ознакомиться по мере
изложения в последующих раз-
делах сайта (см.,например,
разделы "Занимательные
шпаргалки" Mathcad.
Тест Метода № 1. и др.).
Там же приведены рисунки -
таблицы декомпозиции первых
10 натуральных чисел.
При этом суммы декомпозиции
натуральных чисел представле-
ны в виде простых и десятичных
дробей и могут быть проверены
вручную или с помощью школьно-
го калькулятора.
Дополнительно с разно-
образными примерами и вариан-
тами разложения натуральных
чисел в конечные числовые ря-
ды можно ознакомиться на сайте
Алгоритм декомпозиции был
протестирован в системе Math-
cad и показал абсолютную точ-
ность разложения натуральных
и вещественных чисел в части
равенства исходного числа и
его суммы декомпозиции.
В "шапке" сайта расположен
рекламный пример декомпозиции
числа "1" в "наглядном" гра-
фическом представлении для ин-
тервалов n = 1, 2, 3, 4, 5,
6, 7, 8, 9 и 10 .
Так же с результатами те-
стирования с возможностью их
"ручной" проверки можно под-
робно ознакомиться по мере
изложения в последующих раз-
делах сайта (см.,например,
разделы "Занимательные
шпаргалки" Mathcad.
Тест Метода № 1. и др.).
Там же приведены рисунки -
таблицы декомпозиции первых
10 натуральных чисел.
При этом суммы декомпозиции
натуральных чисел представле-
ны в виде простых и десятичных
дробей и могут быть проверены
вручную или с помощью школьно-
го калькулятора.
Дополнительно с разно-
образными примерами и вариан-
тами разложения натуральных
чисел в конечные числовые ря-
ды можно ознакомиться на сайте
Расчётами было установлено,
что различные модели декомпо-
зиции формируют уникальный за-
кон изменения величин расчёт-
ных слагаемых ("составных" чи-
сел) di в составе суммы ряда
разложения относительно своего
среднего значения D/n .
Характерные графики измене-
ния расчётных слагаемых di в
зависимости от первых значений
i для n = 10 приведены в каждом
разделе "Занимательных шпаргалок"
Mathcad.
Также, дополнительно, ана-
логичные графики показаны
при рассмотрении соответству-
ющего Метода декомпозиции в
последующих разделах сайта,
причем для "охвата" и тестиро-
вания Методов на больших интер-
валах разложения n = 365.
В арифметических операци-
ях суммирования используется
только знак +.
Численные значения расчётных
слагаемых di в Методах декомпо-
зиции - НЕ ПОВТОРЯЮТСЯ.
Для демонстрации абсолютной
точности расчётов используются
все значащие цифры результатов
вычислений в браузере.
Тест Метода №1 предлагает модель возрастания численных значений расчётных слагаемых di от i по линейному закону. Ниже, встолбик, представ- лена "занимательная" декомпо- зиция первых девяти натураль- ных чисел такая, что число слагаемых в сумме для каждой декомпозиции равно самому чис- лу (n = D).Для удобства сравнения с показаниями графика строка де- композиции числа 10 представ- лена в десятичных дробях.
На Графике приведено измене- ние численных значений слагаемых di в зависимости от i в составе суммы разложения числа 10 по за- конам декомпозиции "Метода № 1" (возрастание величин расчётных слагаемых суммы декомпозиции по линейному закону).
Результаты расчётов этого раздела "Занимательных шпар- галок" Mathcad легко могут быть проверены вручную. Дополнительно с разно- образными примерами и вариан- тами разложения натуральных чисел в конечные числовые ря- ды можно ознакомиться на сайте
Рассмотрен "шуточный" пример декомпозиции вещественного чис- ла в виде условного МРОТ в раз- мере 10842,75 руб. при раскладе его на 365 дней в году. Ниже на слайде из оригиналь- ных расчетов в системе Mathcad приведен График изменения сла- гаемых di в зависимости от i, а так же "Проверка" конеч- ной суммы декомпозиции.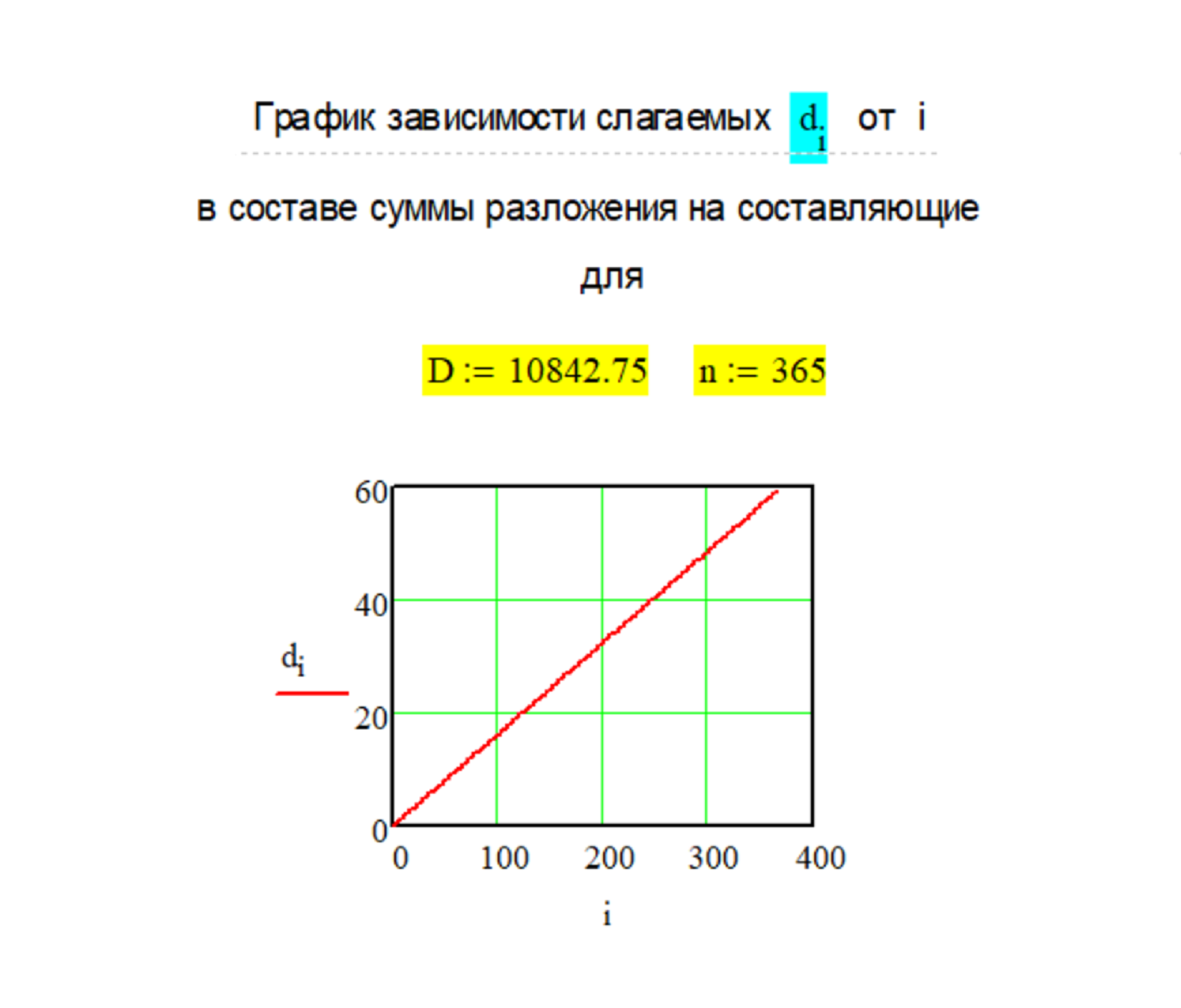
Для корректного определения величины слагаемого на Графике в узловой точке i=200 ниже по тексту приведен соответствующий фрагмент расчёта на сайте слага- емого d1[200] по Методу № 1.
Фрагмент расчета
по Методу № 1.

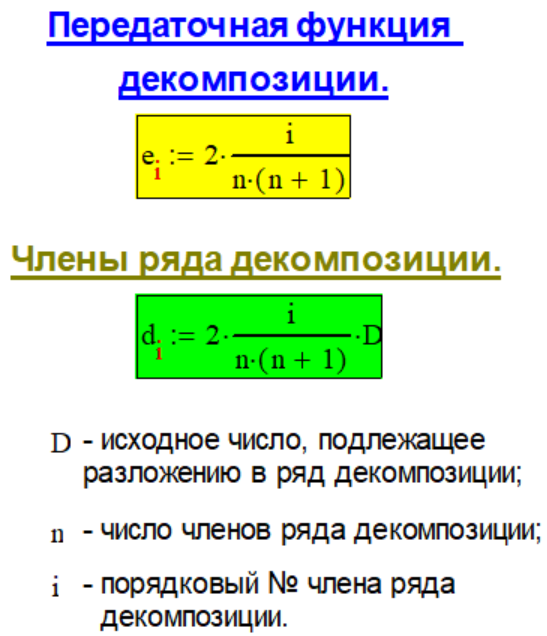
Тест Метода №2 предлагает модель возрастания численных значений расчётных слагаемых di от i по степенному закону. Ниже, встолбик, представле- на "занимательная" декомпози- ция первых девяти натуральных чисел такая, что число слагае- мых в сумме для каждой деком- позиции равно самому чис- лу (n = D).Для удобства сравнения с пока- заниями графика строка декомпо- зиции числа 10 представлена в десятичных дробях.
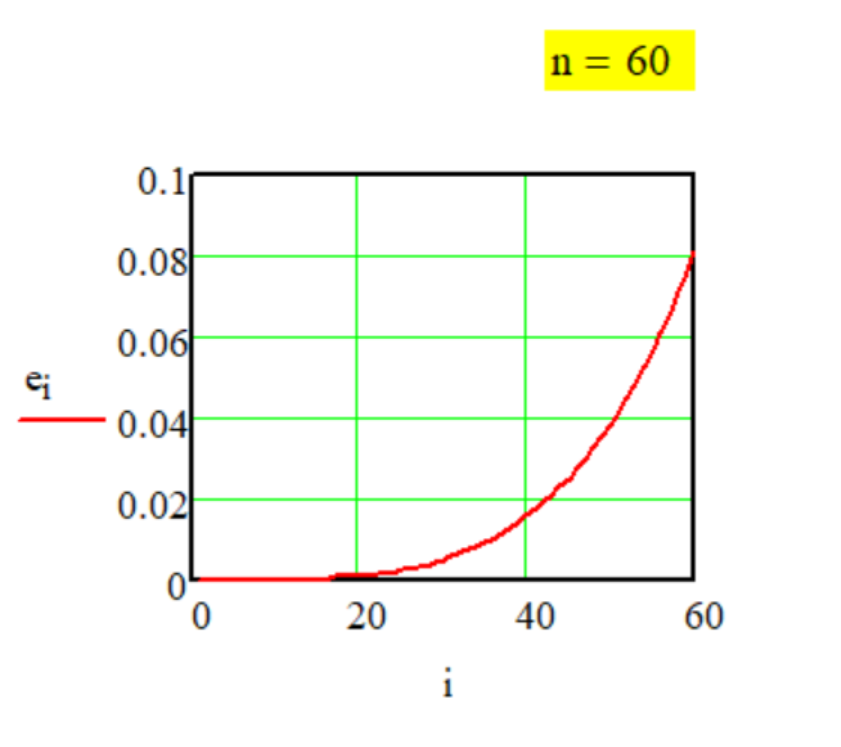
На Графике приведено измене- ние численных значений слагаемых di в зависимости от i в составе суммы разложения числа 10 по за- конам декомпозиции "Метода № 2" (возрастание величин расчётных слагаемых суммы декомпозиции по степенному закону).
Результаты расчётов этого раздела "Занимательных шпар- галок" Mathcad могут быть проверены на калькуляторе. Дополнительно с разно- образными примерами и вариан- тами разложения натуральных чисел в конечные числовые ря- ды можно ознакомиться на сайте
Рассмотрен "шуточный" пример
декомпозиции вещественного чис-
ла в виде условного МРОТ в раз-
мере 10842,75 руб. при раскладе
его на 365 дней в году.
Ниже на слайде из оригиналь-
ных расчетов в системе Mathcad
приведен График изменения сла-
гаемых di в зависимости от i,
а так же "Проверка" конечной
суммы декомпозиции.
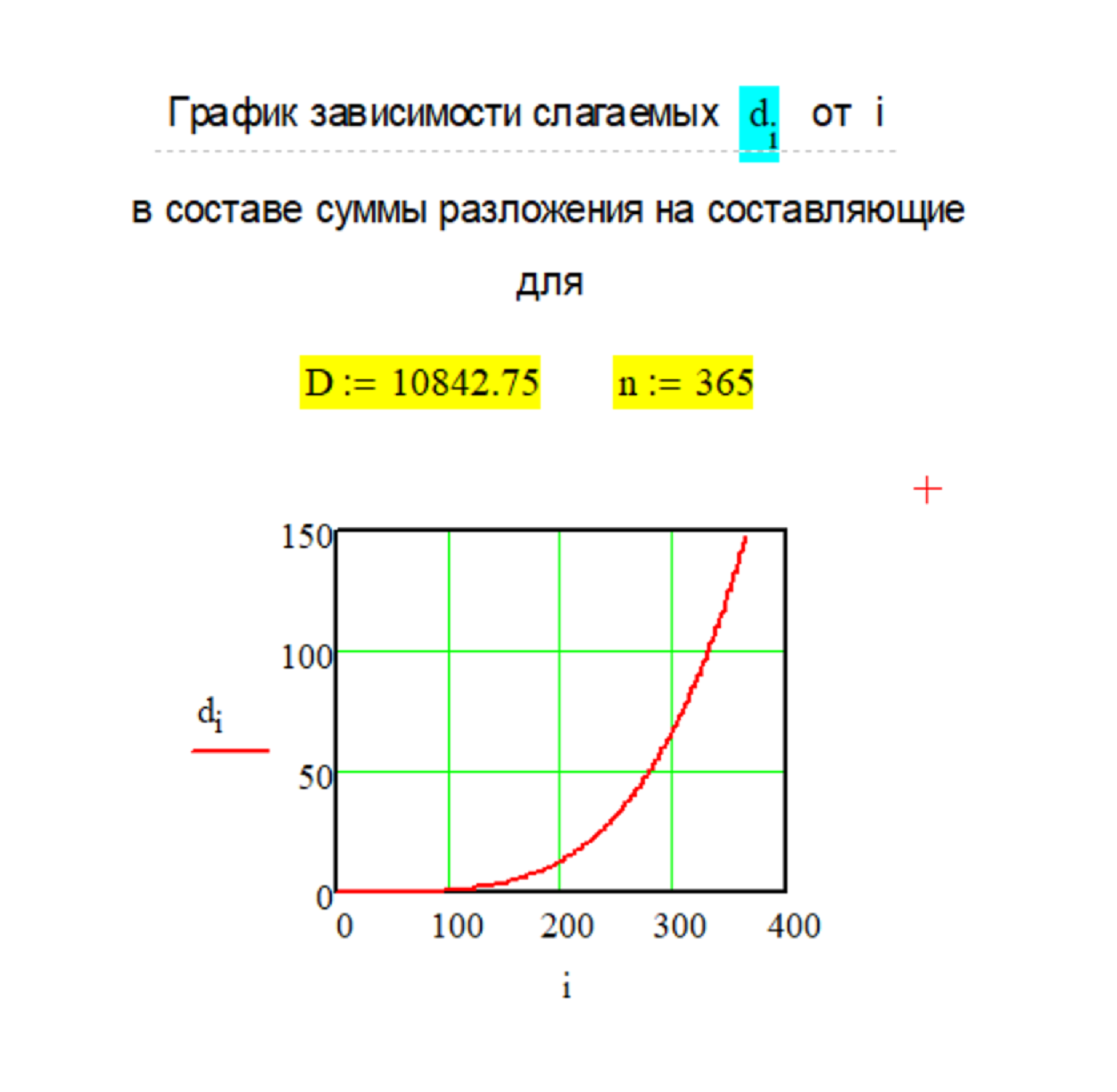
 Для корректного определения
величины слагаемого на Графике
в узловой точке i=300 ниже по
тексту приведен соответствующий
фрагмент расчёта на сайте сла-
гаемого d2[300] по Методу № 2.
Для корректного определения
величины слагаемого на Графике
в узловой точке i=300 ниже по
тексту приведен соответствующий
фрагмент расчёта на сайте сла-
гаемого d2[300] по Методу № 2.
Фрагмент расчета
по Методу № 2.
![Фрагмент расчёта на сайте декомпозиции числа для итерации i[300] по начальным данным расчётного примера Метода № 2.](2023-03-06_7-50-30.png)

Тест Метода №3 предлагает модель убывания численных зна- чений расчётных слагаемых di от i по степенному закону. Ниже, встолбик, представ- лена "занимательная" декомпо- зиция первых девяти натураль- ных чисел такая, что число слагаемых в сумме для каждой декомпозиции равно самому числу (n = D).Для удобства сравнения с по- казаниями графика строка деком- позиции числа 10 представ- лена в десятичных дробях.
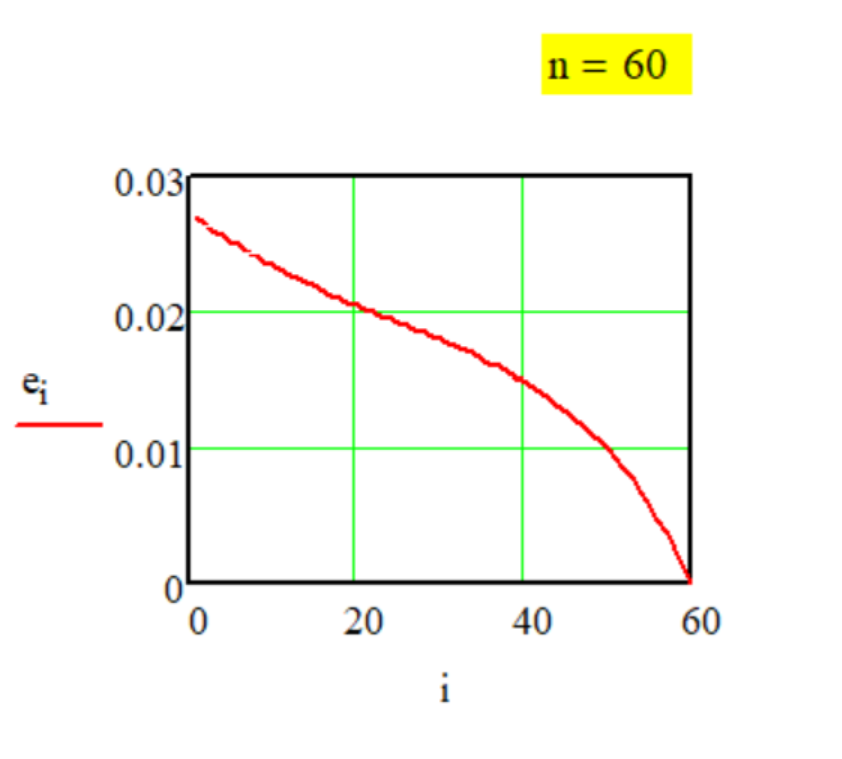
На Графике приведено измене- ние численных значений слагаемых di в зависимости от i в составе суммы разложения числа 10 по за- конам декомпозиции "Метода № 3" (убывание величин расчётных слагаемых суммы декомпозиции по степенному закону).
Результаты расчётов этого раздела "Занимательных шпар- галок" Mathcad могут быть про- верены на калькуляторе. Дополнительно с разно- образными примерами и вариан- тами разложения натуральных чисел в конечные числовые ря- ды можно ознакомиться на сайте
Рассмотрен "шуточный" пример декомпозиции вещественного чис- ла в виде условного МРОТ в раз- мере 10842,75 руб. при раскладе его на 365 дней в году. Ниже на слайде из оригиналь- ных расчетов в системе Mathcad приведен График изменения сла- гаемых di в зависимости от i, а также "Проверка" конечной суммы декомпозиции.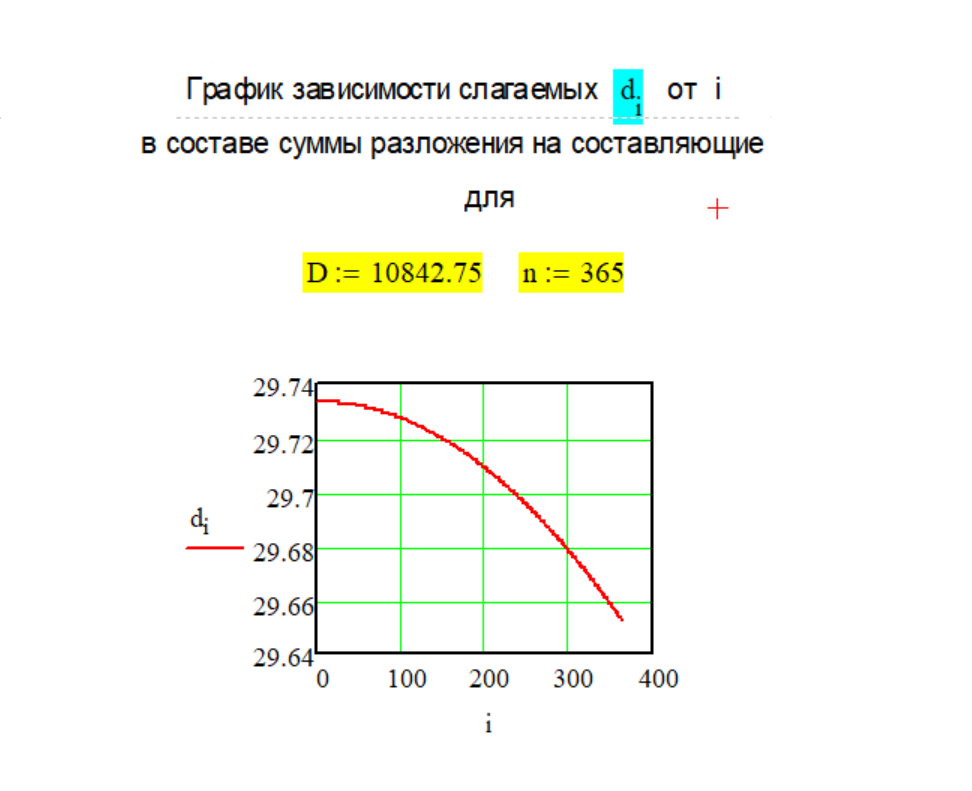
Для корректного определения величины слагаемого на Графике в узловой точке i=300 ниже по тексту приведен соответствующий фрагмент расчёта на сайте сла- гаемого d3[300] по Методу № 3.
Фрагмент расчёта
по Методу № 3.


Как уже указывалось, харак- терной особенностью любого "Метода..." декомпозиции числа является формируемые этими ме- тодами уникальные законы изме- нения абсолютных величин "сос- тавных" расчётных слагаемых di в выражении суммы декомпозиции числа D ( "законы строения числа" ). (См. ранее - линейный закон возрастания, степенной закон убывания "Занимательные шпаргалки"
Mathcad. и т.д.) В символьном виде "реализа- ция" декомпозиции числа D в терминах системы Mathcad мо- жет быть определена следующим выражением числового ряда:,
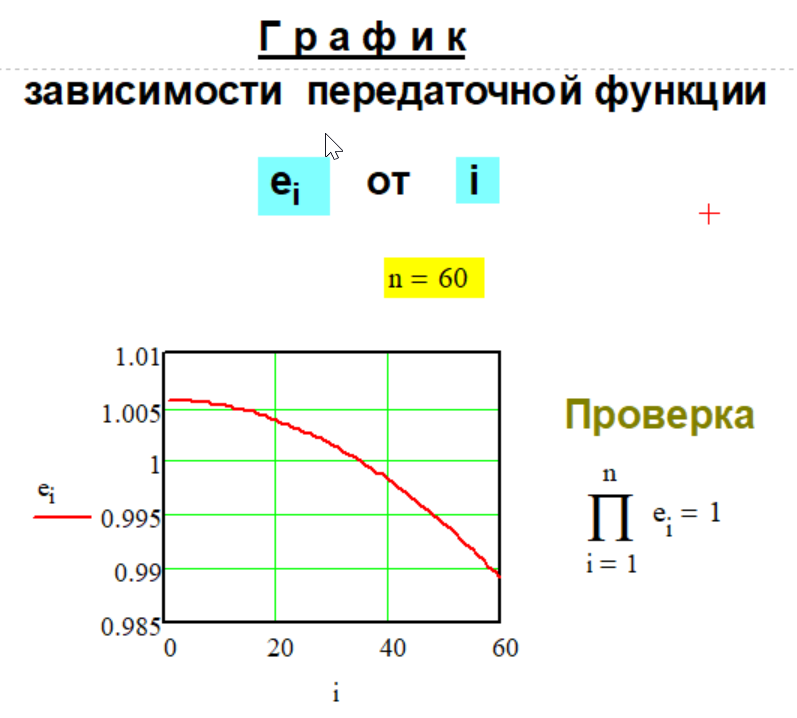
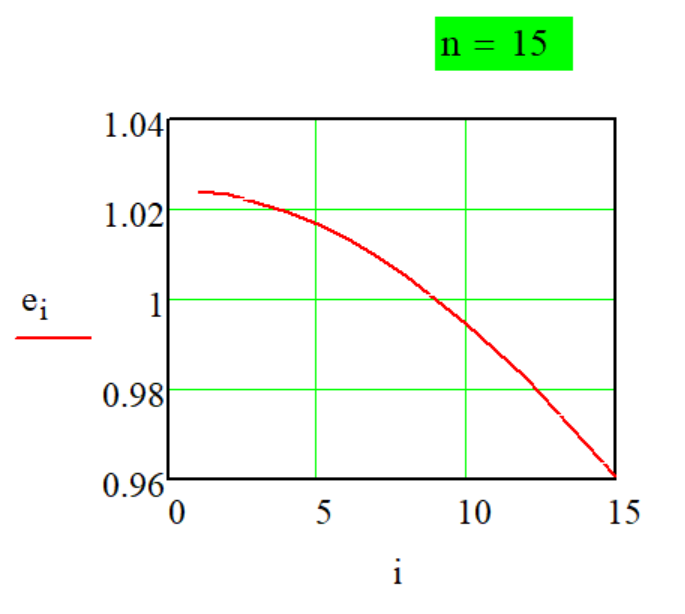
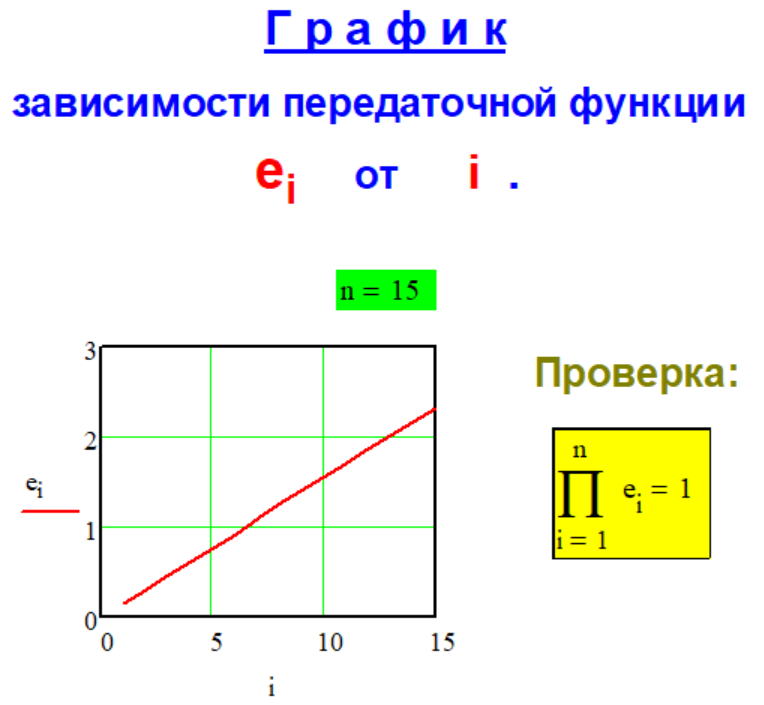
которое включено "гербом" в графическую часть логотипа сайта. Галерея" "Методов...", для компактности, представлена в виде "графики" декомпозиции числа D = 1 . При таком подходе модули- руется, своего рода, "ЕДИНИЧНАЯ" "ПЕРЕДАТОЧНАЯ" функция декомпозиции числа ei и слагаемые декомпозиции числа D di будут определяться простым выра- жением ручного счёта: di = ei * D . Классификация "Методов.." декомпозиции числа пока не составлена, поэтому примеры реализации "Методов..." оформлены в виде каталога графиков эталонной зависи- мости единичных пере- даточных функций декомпозиции числа ei от i . Идея создания, тестирова- ние и выполнение практичес- ких расчётов на базе соот- ветствующей передаточной функции были осуществлены автором в системе Mathcad. "Методы...- mirror" на сай- те не представлены, но могут быть рассмотрены дополни- тельно при обновлении контента сайта. Область применения "Метода.." зависит от выбора (назначения) параметра n , который указан на каждом рисунке применительно к графику соответствующей передаточной функции ei . При выборе другого значения интервала декомпозиции n характер графика может изме- няться. Так же представлена проверка фундаментального свойства передаточной функции ei :,
выполненная в системе Mathcad. Первые три рисунка графиков передаточных функци ei соответствуют расчётным "Методам № 1 - 3" на сайте.
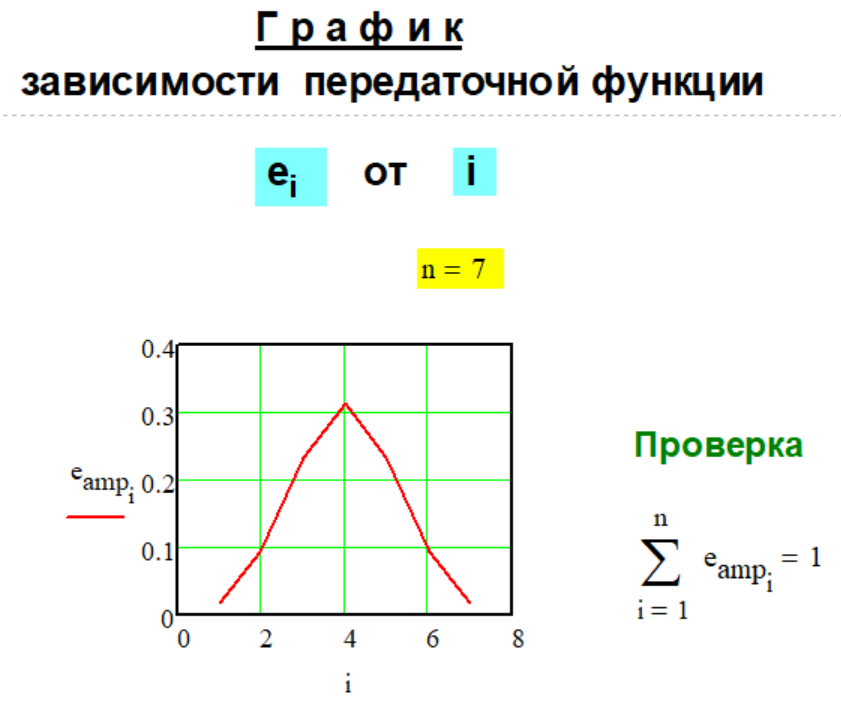
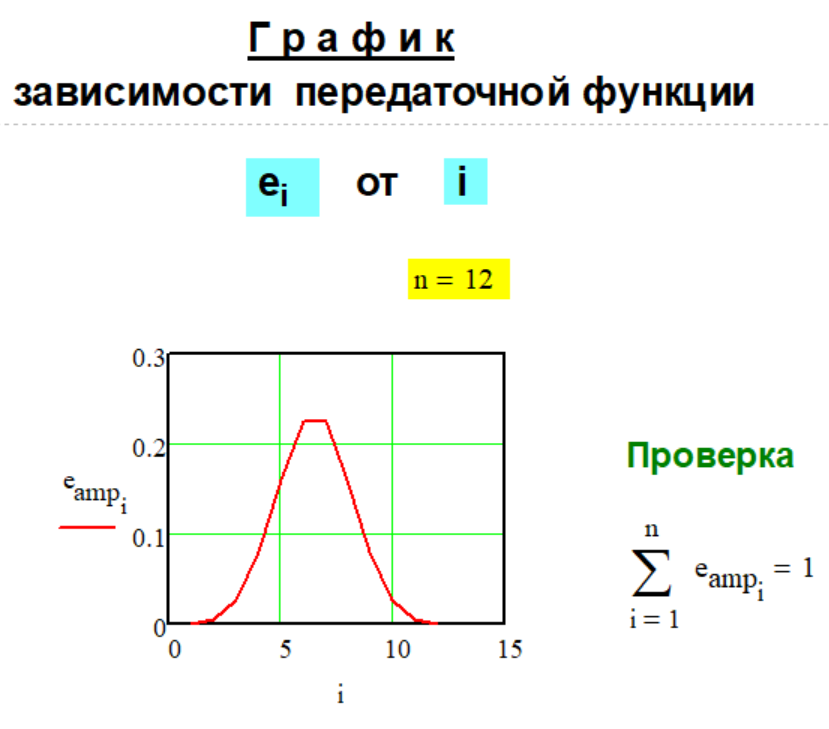
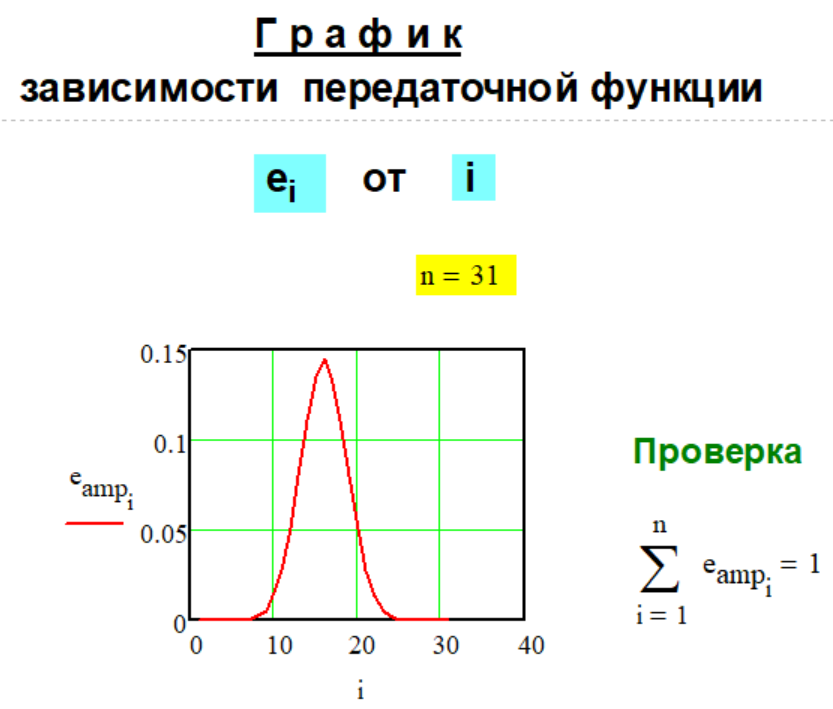
Передаточные функции декомпо- зиции числа "Методов..." каталога за номерами: 1.34. Передаточная функция
Метода G-1-34. 1.35. Передаточная функция
Метода G-1-35. 1.36. Передаточная функция
Метода G-1-36. нашли практическое применение на примере расчётов условного семейного бюджета на сайте: Расчётный пример № 1
n = 7 . Расчётный пример № 2
n = 12 . Расчётный пример № 3
n = 31 . * * *
По аналогии с принципом
построения декомпозиции числа,
когда исходное число представля-
ется эквивалентной по величине
суммой расчётных слагаемых,
ДЕКОМПОЗИЦИЯ ЧИСЛА
СУММОЙ
(СУММИРОВАНИЕМ)
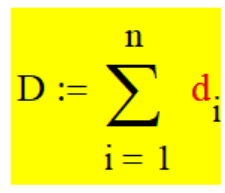 ...(1)
возможна декомпозиция числа в
виде его "разложения" на экви-
валентное произведение ряда
расчётных сомножителей
"многочленное произведение"
ДЕКОМПОЗИЦИЯ ЧИСЛА
...(1)
возможна декомпозиция числа в
виде его "разложения" на экви-
валентное произведение ряда
расчётных сомножителей
"многочленное произведение"
ДЕКОМПОЗИЦИЯ ЧИСЛА
ПРОИЗВЕДЕНИЕМ
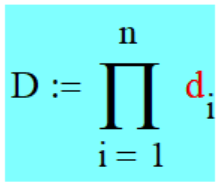 ...(2)
...(2)
Все положения и свойства
декомпозиции числа, рассмотрен-
ные ранее, в полной мере сохра-
няются и в случае
"Декомпозиции
числа произведением" ...(2)
При использовании единичных
передаточных функций декомпози-
ции числа произведением ei
с основным свойством (3)
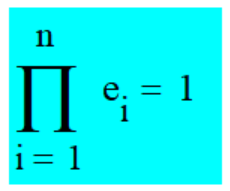 ...(3)
...(3)
рсчётные сомножители di при
декомпозиции числа D на экви-
валентное ПРОИЗВЕДЕНИЕ
будут определяться формулой (4)
di = Math.pow(D,1/n) * ei...(4)
Ниже представлены
графики передаточных
функций
методов
P-1-1, P-1-2, P-1-3. ,
полученных из расчётов
в системе Mathcad.
Практические расчёты
всегда можно выполнить в
разделе "Методов ... "
К А Т А Л О Г
"Методов..."
декомпозиции
числа
произведением.
Графики первых трёх
(стандартных) методов
декомпозиции числа произве-
дением из расчётов в системе
Mathcad приведены ниже.
Передаточная функция
Метода P-1-1
декомпозиции числа
произведением.
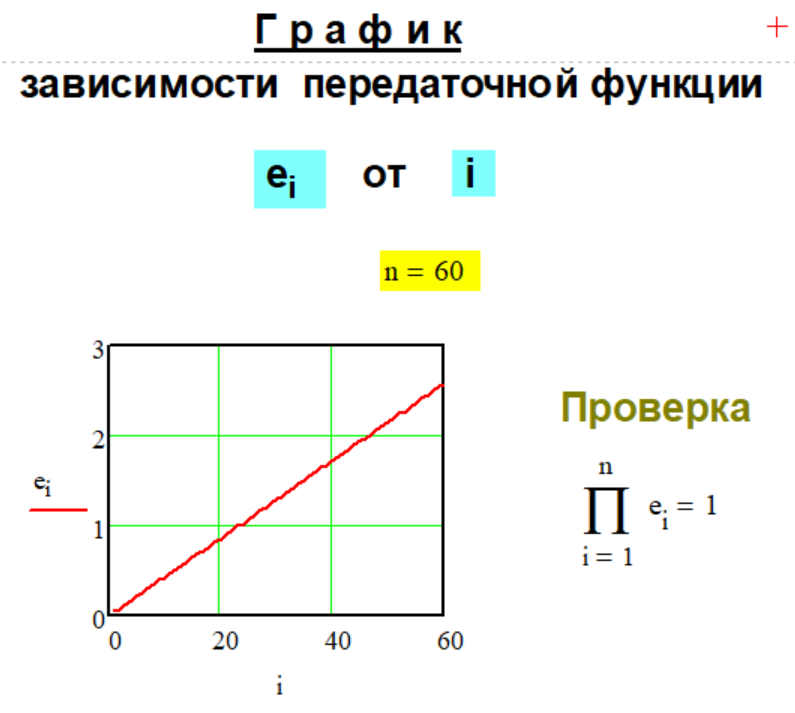
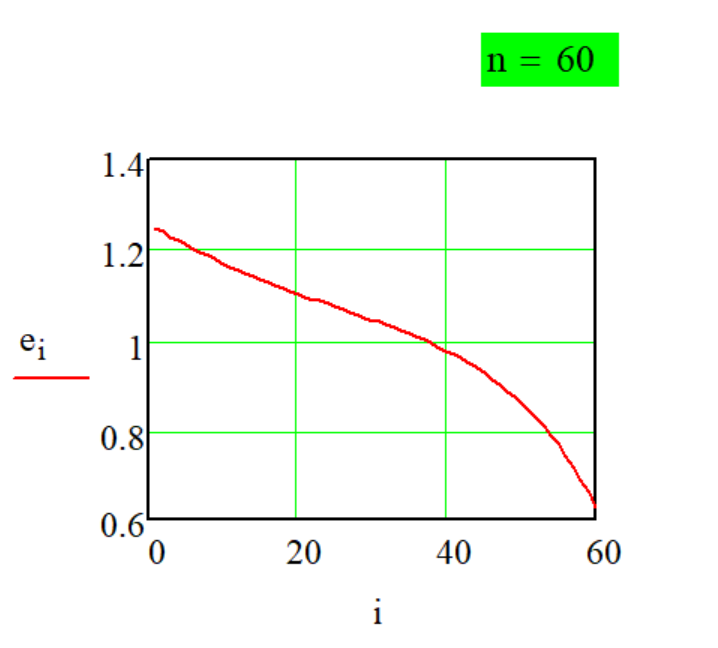
Передаточная функция
Метода P-1-2
декомпозиции числа
произведением.
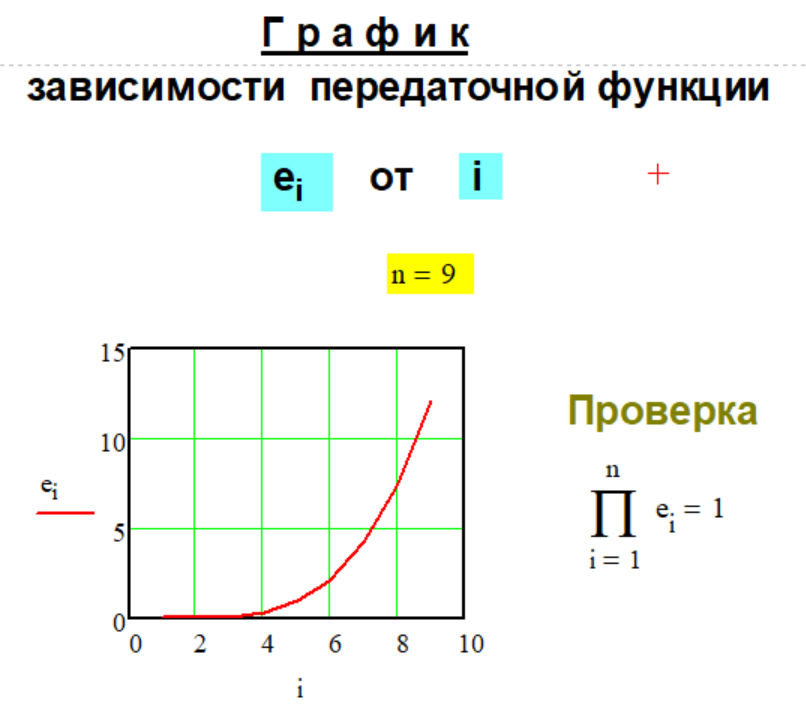
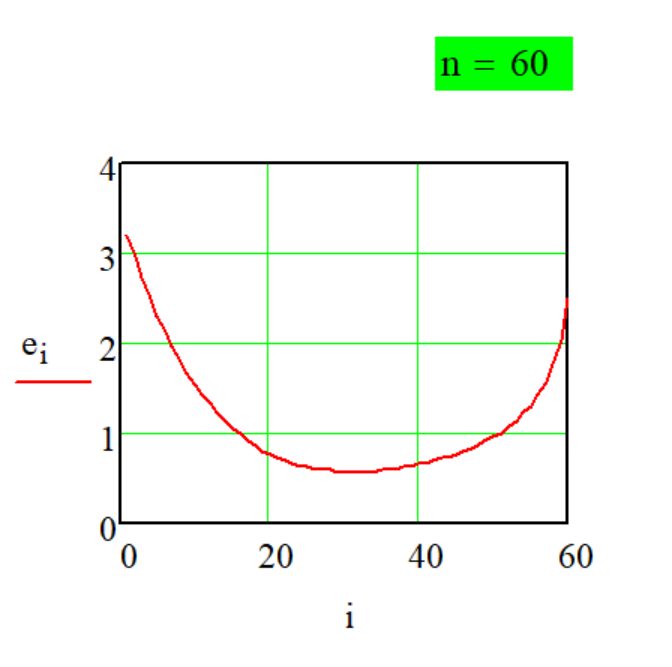
Передаточная функция
Метода P-1-3
декомпозиции числа
произведением.
ДАНО: Имеем в наличии сумму S0 = 1250 руб. 75 коп. ЗАДАНИЕ: 1. Купить 5 (пять) подарков с кэшбеком. 2. Сколько оптимально можно потратить на каждый прдарок? 3. Варианты расчётов. РЕШЕНИЕ: Для решения задачи выполняем декомпозицию исходной суммы S0 = 1250 руб. 75 коп. Например, по "Методу № 1...", принимая за исходные данные расчёта: D1 = 1250.75 , n1 = 6 (с учётом кэшбека). ОТВЕТ: Результаты расчёта, и, возможные варианты ответа - следующие: Величина расчётного слагаемого d1[1]: 59.5595238095238 руб. - можем принять за кэшбек в составе исходной суммы S0 = 1250 руб. 75 коп. ; Величина расчётного слагаемого d1[2]: 119.1190476190476 руб. - можем принять за стоимость подарка № 1 в составе исходной суммы S0 = 1250 руб. 75 коп. ; Величина расчётного слагаемого d1[3]: 178.67857142857142 руб. - можем принять за стоимость подарка № 2 в составе исходной суммы S0 = 1250 руб. 75 коп. ; Величина расчётного слагаемого d1[4]: 238.2380952380952 руб. - можем принять за стоимость подарка № 3 в составе исходной суммы S0 = 1250 руб. 75 коп. ; Величина расчётного слагаемого d1[5]: 297.79761904761904 руб. - можем принять за стоимость подарка № 4 в составе исходной суммы S0 = 1250 руб. 75 коп. ; Величина расчётного слагаемого d1[6]: 357.35714285714283 руб. - можем принять за стоимость подарка № 5 в составе исходной суммы S0 = 1250 руб. 75 коп. ; Реальные расчётные суммы трат П Р И М Е Р А можно изменить "по карману". Разнообразные варианты расчётов всегда можно подобрать в приложенииТакже для индивидуального подхода к решению широкого спектра задач декомпозиции числа рекомендуется
"Метод построения прототипа передаточной функции"
С этой целью определяем / назначаем : D - общий размер (ёмкость) не- распределённого диско- вого пространства, (Мб, ГБ); n - число (количество) требуемых разделов жёсткого диска после его разделения; И выполняем декомпозицию числа D на интервале декомпозиции n с использованием выбран- ного "Метода..." расчёта декомпозиции числа D : D = d1 + d2 +...+ dn , где D - исходный размер (ёмкость) жёсткого диска и d1,d2,... dn - n составляющих его разделов di после разделения (декомпо- зиции). Изложенную процедуру де- композиции числа можем пов- торить применительно к лю- бому полученному разделу жёсткого диска di с целью его дальнейшего раз- деления на подразделы . Разнообразные варианты расчёта декомпозиции числа всегда можно подобрать в приложенииТакже для индивидуального подхода к решению широкого спектра задач декомпозиции числа рекомендуется
"Метод построения прототипа передаточной функции"
* * *
Основной характеристи-
кой и мерой преломляюще-
го свойства линзы служит
её оптическая сила.
Оптическая сила - это
физическая величина, ко-
торая характеризует пре-
ломляющую способность
линзы и оптических систем
линз.
Оптическая сила линзы
обозначается буквой D
и измеряется в диоптриях
(дптр):
D = 1/F ,
где
F - фокусное расстояние
линзы.
Оптическая сила D системы,
состоящей из n тонких
линз, равна алгебраической
сумме оптических сил этих
линз (*):
D = D1 + D2 +...+ Dn (*) ,
где
D1 - оптическая сила
1-й линзы;
D2 - оптическая сила
2-й линзы;
................
Dn - оптическая сила
n-й линзы;
Выполняя декомпозицию
требуемой по техническому
заданию суммарной оптичес-
кой силы D из левой части
выражения (*), автоматически
получаем состав оптических
сил системы n тонких линз
из выражения декомпозиции
числа D (**):
D = d1 + d2 +...+ dn, (**)
где
D,d1,d2,..dn- исходное число,
подлежащее декомпозиции,
и n составляющих
di слагаемых суммы его
декомпозиции (**).
Приравнивая сходственные
слагаемые правых частей вы-
ражений (*) и (**) находим
расчётные значения оптичес-
ких сил Di системы n
тонких линз.
А, именно:
D1 = d1;
D2 = d2;
........
Dn = dn.
Соответственно:
фокусные
расстояния -
F1 = 1/d1;
F2 = 1/d2;
........
Fn = 1/dn.
Для практических и опыт-
ных исследований эффектив-
ным подходом будет исполь-
зование декомпозиции еди-
ничной оптической силы
D = 1 ,
то есть прменение широко-
го спектра единичных пере-
даточных функций декомпо-
зиции числа.
Смотрим, например,
Приложение
 Также для индивидуального
подхода к решению широкого
спектра задач декомпозиции
числа
рекомендуется
Также для индивидуального
подхода к решению широкого
спектра задач декомпозиции
числа
рекомендуется
"Метод
построения прототипа
передаточной функции"
ЭКСПЕРИМЕНТИРУЕМ
для
БЕСПИЛОТНИКОВ
И
ПРИЦЕЛОВ НОЧНОГО
ВИДЕНИЯ !
ПРИМЕЧАНИЕ:
Выражение (**) допуска-
ет произвольную перестанов-
ку слагаемых di .
* * *
В упрощённом виде под урав- нением регрессии будем понимать следующее выражение (1): Y=a1*x1+a2*x2+..+ai*xi+..+an*xn (1), где Y - заданная левая часть уравнения регрессии (1); a1, a2,.., ai,.., an - известные коэффициенты уравнения регрессии (1); x1,x2,..,xi,..,xn - неизвестные уравнения регрессии (1). Или, переобозначая, ai * xi = Yi уравнение регрессии (1) пере- ходит в уравнение вида (1.1): Y= Y1 + Y2 +..+ Yi +..+ Yn (1.1) С другой стороны, раскладывая в ряд декомпозиции число D = Y на интервале декомпозиции n , будем иметь выражение (2): D = d1 + d2 +..+ di +..+ dn (2) откуда, приравнивая, почленно сходственные слагаемые выра- жений (1.1) и (2) Yi равно di находим неизвестные уравнения регрессии xi по формуле (3): xi = di / ai (3).
* * *
По аналогии со схемой реше- ния уравнения регрессии будем создавать "поверх" заданного алгебраического уравнения с n неизвестными xn сходствен- ную суперпозицию эквивалентных блоков DBi , сумма которых заведомо равна нулю. Однородное алгебраическое уравнение с n неизвестны- ми xn (*): k1*x1+k2*x2+..+ki*xi+..+kn*xn=0.(*) Сходственная суперпозиция эквивалентных блоков DBi (**): DB1+DB2+..+DBi+..+DBn=0.(**) На базе решения декомпози- ции числа составление указан- ных эквивалентных блоков DBi можно достигнуть, по крайней мере, тремя способами. СПОСОБ 1. При использовании произ- вольного "Метода..." модули- рования декомпозиции числа D - составление разности между средним D/n и расчётным значениями di слагаемых из состава суммы декомпозиции числа. Например, для расчётно- го "Метода № 1" блок DBi будет иметь следующий вид: DBi =[( D1 / n1 ) - d1(i) ]. СПОСОБ 2. При использовании двух "разноимённых" "Методов..." декомпозиции числа, выполнен- ных при общих значениях n и D - составление разности рас- чётных значений слагаемых суммы декомпозиции каждого метода. Например, для расчётных методов "Метод № 1" и "Метод № 1- mirror" блок DBi будет иметь следующий вид: DBi =[ d1(i) - b1(i) ], где d1(i) , b1(i) - соответственно расчётные слагаемые декомпозиции числа методов "Метод № 1" и "Метод № 1- mirror", найденные при одинаковых начальных условиях (в обозначениях методов n1 = m1 , D1 = B1). СПОСОБ 3. При использовании в рас- чётах декомпозиции числа передаточных функций ei - разность их значений, с коэф- фициентом пропорциональности равным D . Например, для передаточных функций Ei и ei блок DBi будет иметь следующий вид: DBi =[ Ei - ei ] * D . При таком подходе общее выражение для неизвестных xi однородного алгебраического уравнения с n неизвестными будет иметь вид (***): xi = DBi / ki (***), где DBi - эквивалентный блок сходственной суперпо- зиции(**); ki - заданные коэффициенты исходного алгебраи- ческого уравнения (*); i - общие индексы переменных расчёта (также возможны различные "перекрёстные" приравнивания слагаемых). Для практических расчётов будет эффективным применение широкого спектра единичных передаточных функций декомпо- зиции числа e[i] :
Смотрим, например, ПриложениеТакже для индивидуального подхода к решению широкого спектра задач декомпозиции числа рекомендуется
"Метод построения прототипа передаточной функции"
* * *
* * *
Классическим примером деком-
позиции числа является формула
векторной алгебры для квадрата
длины вектора (R).
Изначально
- теорема Пифагора
(для плоского случая
векторной алгебры):
R2 = x2 + y2 + z2 , (*)
где
R, x, y, z - длина вектора и
его проекции на
координатные оси.
Декомпозиция числа D при n=3
будет представлена в следующем
виде
D = d1 + d2 + d3 , (**)
где
D, d1, d2, d3 - исходное число и составляющие
и слагаемые суммы
его ( D ) декомпозиции.
Сравнивая "почленно" форму-
лы (*) и (**) усматриваем их
полную аналогию, при этом
R2 равно D ;
x2 равно d1 ;
y2 равно d2 ;
z2 равно d3 ;
В случае применения деко-
мпозиции числа при n > 3 ,по
сути, переходим из трехмер-
ного векторного пространства
n = 3
- в многомерное
n > 3 .
Тем самым модели и "Мето-
ды..." декомпозиции числа
позволяют устанавлвать разме-
рения векторов в многомерном
векторном пространстве по ана-
логии с трёхмерным (Евклидовым
пространством).
В процессе приравнивания
возможны произвольные пере-
становки слагаемых di в сос-
таве суммы декомпозиции блока
D=R2 в формуле (**).
Применение различных "Ме-
тодов..." декомпозиции числа
открывают новые возможности
моделирования многомерных
векторных полей при их ис-
следовании в различных обла-
стях науки и техники.
Для практических расчётов
будет эффективным применение
широкого спектра единичных
передаточных функций декомпо-
зиции числа e[i] :
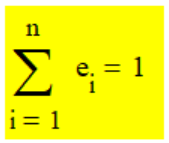
Например,
Приложение
 Также для индивидуального
подхода к решению широкого
спектра задач декомпозиции
числа
рекомендуется
Также для индивидуального
подхода к решению широкого
спектра задач декомпозиции
числа
рекомендуется
"Метод
построения прототипа
передаточной функции"
* * *
Многие фундаментальные по- ложения геометрии и физики свя- заны с математическим числом PI = 3.1415926 . Классическими примерами являются формулы вычисления объ- ёмов тел вращения, углов пово- ротов и т.д., величины которых пропорциональны числу PI . Раскладывая число PI на состав- ляющие с использованием "Мето- дов..." декомпозиции числа получаем абстрактную модель декомпозиции сущности, которая пропорциональна числу PI (*): PI=PI1+PI2+..+PIi+..+PIn.(*) При этом физические законы сохранения количества, сплошности, неразрывности и т.п. применительно к рассматриваемой сущности согласно основному свой- ству декомпозиции числа БУДУТ ВЫПОЛНЯТЬСЯ . Разнообразные варианты расчётов всегда можно подобрать в приложенииТакже для индивидуального подхода к решению широкого спектра задач декомпозиции числа рекомендуется
"Метод построения прототипа передаточной функции"
* * *
В многоступенчатой передаче сложного зубчатого механизма с неподвижными осями общее передаточное отношение равно произведению передаточных отно- шений отдельных ступеней (*): i1,n=i1,2*i2,3*i3,4*...*i(n-1),n (*), где i1,2,i2,3,i3,4,i(n-1),n - передаточные отношения каждой пары колёс (ступеней механизма); n - общее число колёс. Выполняя декомпозицию левой части выражения (*) произведением, находим соответствующие расчётному методу сомножители много- членного произведения, которые могут интерпрети- ровать передаточные отношения каждой пары колёс. Разнообразные варианты расчётов всегда можно подобрать в приложенииТакже для индивидуального подхода к решению широкого спектра задач декомпозиции числа рекомендуется
"Метод построения прототипа передаточной функции"
* * *
Под единичным рядом будем понимать конечный числовой ряд, сумма членов которого равна 1 . Таким свойством "обладают" ряды декомпозиции числа 1 или, другими словами, единичные передаточные функции ei , неоднократно рассмотренные в предыдущих разделах сайта. Напомним, что основным свойст- вом ei , как раз, является ра- венство единице суммы всех i -х членов:!-- ! -->(*)
В теории вероятности осново- полагающим постулатом является положение о суммировании вероят- ностей наступления событий, которые образуют полную группу (т. е. хотя бы одно из событий этой группы произойдёт) (**): p1+p2+p3+...+pi+...+pn = 1 (**), где pi - вероятность наступления i-го события; n - число событий в полной группе. Сравнивая выражения (*) и (**) усматриваем полную аналогию между ei и pi . Для практических расчётов будет эффективным применение широкого спектра единичных передаточных функций декомпо- зиции числа ei , разнообразные законы изменения которых всегда можно подобрать в Приложении российского магазина приложений
Также для индивидуального подхода к решению широкого спектра задач декомпозиции числа рекомендуется
"Метод построения прототипа передаточной функции"
Проверка гипотезы суммиро- вания вероятностей выражения (**) в терминах ei выполняется в PWA-приложении "Галерея "Методов..." декомпозиции числа" для каждого выбранного варианта расчёта передаточной функции. * * *
Закон сохранения электричес-
кого заряда утверждает,что алге-
браическая сумма зарядов замкну-
той системы (системы без обмена
зарядами с внешними телами) оста-
ётся постоянной (1):
q1 + q2 + q3 +..+ qi +..+ qn
равно
const
... (1),
где
qi - i-ый заряд
замкнутой системы;
n - число зарядов
замкнутой системы;
const - произвольная
постоянная
(размерность [кулон]).
Можем поставить себе цель
построить замкнутую систему
зарядов, удовлетворяющую за-
кону сохранения электричес-
ких зарядов (1).
С этой целью будет достаточ-
ным выполнить декомпозицию пра-
вой части const закона сохра-
нения (1), принимая в расчётах:
D = const - исходное число
декомпозиции;
n - интервал
декомпозиции ( число зарядов
замкнутой системы );
Удобно выполнять декомпозицию
с помощью передаточных функций
ei ,
назначая, при этом,
D = 1
( в нашем случае 1, кулон ).
Сумма декомпозиции после рас-
чёта будет иметь вид (2):
d1 + d2 + d3 +..+ di +..+ dn
равно
1
... (2),
где
di - i-ое слагаемое
расчётной суммы декомпозиции
исходного числа D = 1 ;
n - интервал
декомпозиции (назначенное при
расчёте число слагаемых суммы
декомпозиции);
Сравнивая выражения (1) и (2)
усматриваем полную аналогию
между
di и qi ,
то есть
di равно qi
Возможно последовательно
усложнять систему зарядов,
повторно рассматривая деком-
позицию зарядов предыдущего
состояния системы.
Например, выполнить дополни-
тельную декомпозицию зарядов
q1 , q3 :
q1,1 + q1,2 + q1,3 = q1 ,
q3,1 + q3,2 = q3 ,
где
q1,1 , q1,2 , q1,3 - состав
заряда q1 (при n = 3);
q3,1 , q3,2 - состав
заряда q3 (при n = 2).
Для практических расчётов
будет эффективным применение
широкого спектра единичных
передаточных функций декомпо-
зиции числа ei :
Смотрим, например,
Приложение
в
российском
магазине приложений

 Также для индивидуального
подхода к решению широкого
спектра задач декомпозиции
числа
рекомендуется
Также для индивидуального
подхода к решению широкого
спектра задач декомпозиции
числа
рекомендуется
"Метод
построения прототипа
передаточной функции"
* * *
Декомпозицию числа D1 на интервале n1 , расчитанную по Методу № 1 с линейным законом изменения слагаемых d1[i] суммы декомпо- зиции, легко можем интерпрети- ровать как "прохождение" рас- стояния D1, м за n1, секунд . При этом, очевидно : d1[1] - расстояние, пройденное за "1-ю" секунду движения; d1[n] - расстояние, пройденное за "n-ю" секунду движения. Тогда скорость движения V, м/сек , "набранная" при старте на отрезке D, м за вре- мя "разгона" n секунд может быть вычислена по формуле элементарной физики для линейного закона изменения скорости движения тела (*): V =(d1[n] - d1[1])/(n - 1) (*) Для приближённых расчё- тов можем использовать не- линейные методы декомпози- ции расстояния D, м на начальных участках движения: Метод № 2, Метод № 3-mirror и др., принимая малые значения временного интервала "разгона" n = 3-5 секунд. При n = 2 формула (*) упрощается и начальная "стартовая" скорость при использовании Метода № 1 будет определяться простым выражением (**), V = d1[2] - d1[1] (**) представляющем собой разность второго и перво- го "шага" декомпозиции общего заданного тесто- вого расстояния D1, м . Указанная формула (**) определения начальной "стартовой" скорости будет справедлива для любого расчётного Метода декомпозиции. Разнообразные варианты расчётов всегда можно подобрать в приложенииТакже для индивидуального подхода к решению широкого спектра задач декомпозиции числа рекомендуется
"Метод построения прототипа передаточной функции"
* * *
Под "магазином" сопро- тивлений в электрической цепи будем понимать груп- пу сопротивлений, состо- ящую из n резисторов (проводников), соединён- ных последовательно или параллельно. При этом расчёт сопро- тивления "магазина" R, ом выполняется по следующим формулам: - при последовательном соединении проводников; R = R1 + R2 +...+ Rn - при параллельном соединении проводников; 1/R = 1/R1 + 1/R2 +...+ 1/Rn , где R1 , R2 ... Rn - сопро- тивления проводников. Выполняя декомпозицию D применительно к требуемому сопротивлению "магазина" R (или 1/R ), находим сход- ственные по номерам сопро- тивления резисторов из состава суммы декомпозиции блоков : Блок D = R - при после- довательном соединении проводников: R1 = d1 ; R2 = d2 ; ........... Rn = dn ; Блок D = 1/R - при парал- лельном соединении проводников: R1 = 1/d1 ; R2 = 1/d2 ; ........... Rn = 1/dn. Полная аналогия существует при расчётах емкостей C и индуктивностей L электрических цепей. Приведём лишь формулы расчёта - для параллельных цепей: C = C1 + C2 +...+ Cn , 1/L = 1/L1 + 1/L2 +...+ 1/Ln - для последовательных цепей: L = L1 + L2 +...+ Ln , 1/C = 1/C1 + 1/C2 +...+ 1/Cn где C1 , C2 ... Cn - ёмкости конденсаторов; L1 , L2 ... Ln - индуктив- ности катушек. Методы декомпозиции числа применимы также при расчёте общего напряжения цепи U при последовательном соедине- нии проводников: U = U1 + U2 +...+ Un где U1 , U2 ... Un - напряжения на концах проводников. При этом по требуемому на- пряжению U и заданному ко- личеству n проводни- ков устанавливается напряже- ние на концах каждого провод- ника в соответствии с выбран- ным расчётным Методом деком- позиции числа. Разнообразные варианты решения задач на декомпозицию числа всегда можно подобрать в ПриложенииТакже для индивидуального подхода к решению широкого спектра задач декомпозиции числа рекомендуется
"Метод построения прототипа передаточной функции"
* * *
Под "планировкой" заданной общей площади S0, м2 будем понимать оптимальную "разбив- ку" этой площади на составля- ющие её части si, м2 . С этой целью, как нельзя кстати, подходит любой из рас- смотренных на сайте "Метод де- композиции..." числа. При этом достаточно выпол- нить декомпозицию площади ве- личиной в 1 м2 и результат умножить на значение общей площади S0, м2 . Сумма площадей участков де- композиции si, м2 однозначно совпадёт с первоначальной площадью "планировки" S0, м2 . Соотношение площадей участ- ков si достигается разнообраз- ным выбором "Методов декомпози- ции...", а также непосред- ственным назначением числа n - количества участков при "планировке" (декомпозиции) общей площади S0, м2 . В качестве примера рассмат- ривается "планировка" жилой площади 2-х этажного дома с мансардой. Выбираем число комнат: - на 1-м этаже - 7 комнат; - на 2-м этаже - 5 комнат; - на мансарде - 3 комнаты. Для декомпозиции 1 м2 жилой площади 1-го этажа выбираем расчётный "Метод № 1" декомпози- ции числа, принимая за n1 = 7 . Результаты расчёта на сайте по "Методу № 1" при D1 = 1 n1 = 7 d1[1] = 0.03571428571428571 м2; d1[2] = 0.07142857142857142 м2; d1[3] = 0.10714285714285714 м2; d1[4] = 0.14285714285714285 м2; d1[5] = 0.17857142857142858 м2; d1[6] = 0.21428571428571427 м2; d1[7] = 0.25 м2. Для декомпозиции 1 м2 жилой площади 2-го этажа выбираем расчётный "Метод № 2" декомпози- ции числа, принимая за n2 = 5 . Результаты расчёта на сайте по "Методу № 2" при D2 = 1 n2 = 5 d2[1] = 0.025331724969843185 м2; d2[2] = 0.025331724969843185 м2; d2[3] = 0.07358262967430639 м2; d2[4] = 0.24246079613992763 м2; d2[5] = 0.6332931242460795 м2. Для декомпозиции 1 м2 жилой площади мансарды выбираем расчётный "Метод № 3" декомпози- ции числа, принимая за n3 = 3 . Результаты расчёта на сайте по "Методу № 3" при D3 = 1 n3 = 3 d3[1] = 0.3686418458311484 м2; d3[2] = 0.3340325117986366 м2; d3[3] = 0.29732564237021497 м2. При одинаковой общей площади каждого этажа и мансарды величиной, например, S0 = 100, м2 площади комнат будут составлять НАПРИМЕР: - 1-й этаж 3-я комната S3 = 10.714 м2; - 2-й этаж 5-я комната S5 = 63.329 м2; - мансарда 1-я комната S1 = 36.864 м2; и т. д. На практике приходится выполнять более "тонкую" планировку площадей, учи- тывая дополнительные "не- производственные/нежилые" участки площади. Для земельного участка: - границы участка; - дорожки; - тропинки; - "полянки" и т.п. Для жилого дома: - кухня; - производственные помещения; - коридоры; - тамбуры; - выгородки и т.д. При этом ПРИНЦИП ДЕКОМПОЗИЦИИ 1 м2 при планировке площадей - НЕ МЕНЯЕТСЯ! Разнообразные варианты практического решения задач на декомпозицию числа всегда можно подобрать в ПриложенииТакже для индивидуального подхода к решению широкого спектра задач декомпозиции числа рекомендуется
"Метод построения прототипа передаточной функции"
* * *
Широкий спектр разработан- ных на сайтах "Методов декомпозиции числа" может являться стабильным гене- ратором шифрованных числовых данных - суть новая Энигма . В качестве портативного ге- нератора выбираем по собствен- ному усмотрению произвольный расчётный метод декомпозиции числа PWA-приложения. За исходные данные генерации/кодировки поролей/ключей/координат НАЗНАЧАЕМ: № / индекс расчётного метода (или передаточной функции) де- композиции числа, на базе которых должна быть выполне- на "шифровка / дешифровка" информации. D - исходное число декомпозиции; n - интервал декомпозиции числа; i - порядковый номер итерации декомпозиции числа. Также усложнит пароль собственное переобозначение названия метода расчёта: например, G-1-1 -> Па-013-фУ5 ; P-1-33 -> Lx-p18-nu4 ; PG-1-7 -> Xz-y32-12s и т.д. Для шифровки/дешифровки координат Д О П О Л Н И Т Е Л Ь Н О обозначаем: *x / x* - порядковый номер цифры до/после запятой в результатах расчёта слагаемого декомпозиции d[i] (суть - трбуемое шифруемое цифровое значение); *y / y* - порядковый номер цифры до/после запятой в результатах расчёта "текущей" суммы декомпо- зиции sum[i] (суть - трбуемое шифруемое цифровое значение); Назначение и выбор порядка следования и сочетание исходных параметров расчета - привилегия администратора. На усмотрение администрато- ра расчитанная при заданных шифрованных начальных условиях выбранного метода декомпози- ции числа пара значений " d[i] " / " sum[i] " суть пара терминов "пароль" / "ключ", или - наоборот. СИМВОЛЬНАЯ КОДИРОВКА пароля/ключа (от администратора):№/индекс,D,n,iПРИМЕР кодировки пароля (от администратора):G-1-1,1,3,2РАСШИФРОВКА символов (слева на право): G-1-1 - генерация пароля на базе передаточной функции Метода G-1-1; 1 - исходное число декомпозиции при кодировке, D=1 ; 3 - интервал декомпозиции при кодировке, n=3 ; 2 - порядковый номер итерации расчёта декомпозиции при кодировке, i=2 ; ПАРОЛЬ/КЛЮЧ на смартфоне клиента: (после расчёта онлайн): Величина расчётного слагаемого d[2]=0.3333333333333333 "Текущая" сумма расчётных слагаемых sum[2]=0.5 d[2]=0.3333333333 - пароль (расчётное слагаемое декомпозиции d[2]=0.3333333333); sum[2]=0.5 - ключ ("текущая" сумма декомпозиции sum[2]=0.5); ШИФРОВКА/ДЕШИФРОВКА боевых координат. СИМВОЛЬНАЯ КОДИРОВКА КООРДИНАТ (от администратора):№/индекс,D,n,i,x*,y*На дисплей оператора беспилотника поступили шифрованные данные бое- вых координат. Ш И Р О Т Ы:G-1-3,15,7,2,1*,1*Д О Л Г О Т Ы:G-1-3,15,7,3,3*,5*Для дешифровки координат оператор выполнил расчет декомпозиции числа при следующих исходных данных, полученных из "шифровки": G-1-3 - дешифровка данных должна быть выполнена на базе передаточной функции Метода G-1-3; 15 - исходное число декомпозиции при расшифровке, D=15 ; 7 - интервал декомпозиции при расшифровке, n=7 ; 2 - порядковый номер итерации декомпозиции при расшифровке ШИРОТЫ, i=2 ; 3 - порядковый номер итерации декомпозиции при расшифровке ДОЛГОТЫ, i=3 ; Были получены следующие результаты расчётов деком- позиции на смартфоне, для координаты ШИРОТЫ: Величина расчётного слагаемого d[2]=2.235833421985929; "Текущая" сумма расчётных слагаемых sum[2]=4.491161870240797. По кодировке значащих цифр для ШИРОТЫ x=1*; y=1* находим истинную (дешифрованную) боевую координату ШИРОТЫ 24 для координаты ДОЛГОТЫ: Величина расчётного слагаемого d[3]=2.2041107461045195; "Текущая" сумма расчётных слагаемых sum[3]=6.695272616345316. По кодировке значащих цифр для ДОЛГОТЫ x=3*; y=5* находим истинную (дешифрованную) боевую координату ДОЛГОТЫ 47 БОЕВЫЕ КООРДИНАТЫ (на земле) ШИРОТА/ДОЛГОТА:24/47На карте (после поиска по координатам) точка 24 с.ш. 47 в.д. - окрестность Эр-Рияда, Саудовская Аравия - случайное совпадение. Разнообразные варианты практического решения задач на декомпозицию числа всегда можно подобрать в ПриложенииТакже для индивидуального подхода к решению широкого спектра задач декомпозиции числа рекомендуется
"Метод построения прототипа передаточной функции"
Стабильность расчётов на смартфоне всегда ГАРАНТИРОВАНА! Шифруйте координаты. Изменяйте пароль/ключ Каждый день - утром и вечером! Генератор расчётов деком- позиции числа ВСЕГДА РАБОТАЕТ на сайте:
Methods
of the
Number Decomposition.
Made in Russia.
Z * * *
Анализ результатов рас-
чёта декомпозиции числа сум-
мой показал возможность
простого перехода (пересчёта)
от
декомпозиции числа суммой
к
декомпозиции Т О Г О Ж Е числа
произведением.
Формула пересчёта по опре-
делению расчётного сомножи-
теля p[i]
декомпозиции числа произведе-
нием произвольного числа
D
будет иметь вид (1):
p[i] = sum[i] / sum[i-1] ...(1),
где
sum[i], sum[i-1] - значения
"текущих" сумм на i -м и
i-1 -м шаге итерации
декомпозиции числа суммой;
При этом принимается
sum[0] равно 1 (единице),
то есть величины первых
расчётных слагаемых и
сомножителей сходственных
декомпозиций одного и того
же числа D равны:
d[1] равно p[1],
И
все соответствующие графики
расчётных величин зависимос-
тей от i начинаются
из "общей" точки.
Формулa (1) легко
проверяется расчётами на
сайте для любого "Метода..."
декомпозиции числа суммой
и может быть использована
для ручного расчёта деком-
позиции того же числа про-
изведением.
Особенно просто выполня-
ются расчёты при малых
значениях n .
М Е Т О Д Ы
пересчёта
декомпозиции
числа произведением
от
декомпозиции суммой.
основаны
на базе
классических "Методов.."
расчёта декомпозиции
числа суммой.
Название метода форми-
руется добавлением
литеры "P"
к
названию метода-прототипа,
например,
G-1-1 -> PG-1-1
И Т. Д.
Практические расчёты
всегда можно выполнить в
разделе "Методов пересчета... "
М Е Т О Д Ы
пересчёта
декомпозиции
числа произведением
от
декомпозиции суммой.
* * *
Ниже приведены "рабочие" блоки расчетов изменения декомпозиции числа во времени, полученные из "стандартных" блоков декомпозиции числа суммой G-1-1, G-1-2, G-1-3 путём замены переменной i -> i * Δt где Δt - шаг по времени наблюдения горизонтальной шкалы графиков.
Передаточная
функция
Метода TG-1-1.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х.
Шкала узловых точек
изменения слагаемых
декомпозиции числа
во времени.
Г Р А Ф И К
с у м м ы
с л а г а е м ы х.
Шкала узловых точек
изменения слагаемых
декомпозиции числа
во времени.
Передаточная
функция
Метода TG-1-2.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х.
Шкала узловых точек
изменения слагаемых
декомпозиции числа
во времени.
Г Р А Ф И К
с у м м ы
с л а г а е м ы х.
Шкала узловых точек
изменения слагаемых
декомпозиции числа
во времени.
Передаточная
функция
Метода TG-1-3.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х.
Шкала узловых точек
изменения слагаемых
декомпозиции числа
во времени.
Г Р А Ф И К
с у м м ы
с л а г а е м ы х.
Шкала узловых точек
изменения слагаемых
декомпозиции числа
во времени.
ДОПОЛНИТЕЛЬНО
ВАШИ
варианты
( при n >3 )
задания
прототипа
передаточной
функции
изменения
декомпозиции
числа во времени
можно
РЕАЛИЗОВАТЬ
в
приложении
российского
магазина
приложений


Логарифмируя результат декомпозиции числа 1 произведением, получаем суть декомпозицию числа 0 суммой. В "шапке" сайта приведены фрагменты Декомпозиции нуля, полученные из расчётов в системе Mathcad на базе Методов P-1-1, P-1-2 и P-1-3 декомпозиции числа произведением для D=1 . Ниже на их основе для практических расчётов (и ознакомления) представлены соответствующие методы Z-1-1, Z-1-2, Z-1-3 "Методы декомпозиции нуля" .
Метод Z-1-1
декомпозиции
нуля
от
передаточной
функциии
Метода P-1-1.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х.
№№ слагаемых
декомпозиции числа
Н О Л Ь .
Г Р А Ф И К
с у м м ы
с л а г а е м ы х.
№№ слагаемых
декомпозиции числа
Н О Л Ь .
Метод Z-1-2
декомпозиции
нуля
от
передаточной
функциии
Метода P-1-2.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х.
№№ слагаемых
декомпозиции числа
Н О Л Ь .
Г Р А Ф И К
с у м м ы
с л а г а е м ы х.
№№ слагаемых
декомпозиции числа
Н О Л Ь .
Метод Z-1-3
декомпозиции
нуля
от
передаточной
функциии
Метода P-1-3.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х.
№№ слагаемых
декомпозиции числа
Н О Л Ь .
Г Р А Ф И К
с у м м ы
с л а г а е м ы х.
№№ слагаемых
декомпозиции числа
Н О Л Ь .
ДОПОЛНИТЕЛЬНО
ВАШИ
варианты
( при n >3 )
задания
прототипа
передаточной
функции
декомпозиции
числа НОЛЬ
можно
РЕАЛИЗОВАТЬ
в
приложении
российского
магазина
приложений


Бедняк построил свою стра- тегию возврата денег ДЖИННУ по Методу №1. В качестве суммы кредита D1 он взял 100000 динаров. Полная луна пришлась на 28 ночь - и он принял n1 = 28 . Когда появился ДЖИНН:
ОН
ВЫПОЛНИЛ!
Р А С Ч Ё Т:
* * *

Алгоритм решения "Приложения..." Потребительская корзина. Расчёт. российского магазина приложенийможет быть интерпретирован в виде выражения суммирования (*) с наперёд заданной (известной) правой частью S С У М М Ы ряда i-х парных произведений двух сомножителей, одни из кото- рых (на выбор) известны, а другие - подлежат определению. При этом общее число слагаемых "парных произведений" n назначается зарание по условиям задачи. Для "Приложения..." в его графической части расчёта предусмотрено максимальное значение n = 110 , в расчётной части n - неограниченно и обу- словлено только мощностью системы и временем расчёта: при n = 365 расчёт на ПК занимает около 15 минут. Ряд известных (задаваемых) параметров с присвоенными им номерами ( №№ ) 1...i...n по порядку вводятся в расчёт посредством окна индивидуаль- ного ввода исходных данных пользователем Ц Е Н А .
В "Приложении..." российского магазина приложений
Потребительская корзина. Расчёт. по заданной цене товаров ci и S - назначенной общей стоимости потребительской корзины находятся соответствующие количества товаров qi. [ Возможна и обратная задача, когда мы на рынке хотим "срубить деньжат", например 1000 руб. , реализовав следующее количество товара (в кГс ): q1 = 10; q2 = 15; q3 = 27.8; Назначая в качестве заданной прибыли S = 1000; и вводя в качестве заданных переменных в окно ввода Ц Е Н А веса товаров за номерами i = 1, 2, 3 находим соответствующие "заказанной" В Ы Р У Ч К Е цены товаров за номерами i = 1, 2, 3 c1 = 9.109 ; c2 = 13.663 ; c3 = 25.322 ; П Р О В Е Р О Ч К А 10*9.109+5*13.663+27.8*25.322 = =999.999 ] Аналогичное (типичное) строение имеют многочисленные алгоритмы задач, физический смысл которых усматривается из расшифровки переменных, входящих в алгоритм. Размерности переменных устанав- ливются из условий задачи. Все они (эти алгоритмы) легко могут быть разрешены на базе А Л Г О Р И Т М А Приложения RuStore Потребительская корзина. Расчёт., путём соответствующего вы- бора (назначения) аналогичных переменных схожих алгоритмов. Правая часть алгоритма должна быть известна и , как правило, варьируется в процессе расчё- тов для получения оптимального по условиям задачи соотношения величин входящих параметров. Предложенный в "Приложении..." алгоритм решения является, по сути, единственным возможным ва- риантом ЭКСПРЕСС-РЕШЕНИЯ поставленной задачи в первом приближении, которая в дальней- шем может быть уточнена. При этом все расчёты выполня- ются с А Б С О Л Ю Т Н О Й точностью с проверкой обратного суммирования методами декомпози- ции числа. В выборе назначений статуса ИЗВЕСТНЫЙ/НЕИЗВЕСТНЫЙ параметры алгоритмов РАВНОПРАВНЫ . Ниже рассмотрены некоторые примеры типичных алгоритмов решения практических задач. П Р И М Е Р Ы А Л Г О Р И Т М О В О С Н О В Н Ы Х С Ф Е Р Д Е Я Т Е Л Ь Н О С Т И Ч Е Л О В Е К А.
СОЦИАЛЬНАЯ СФЕРА.
% % % % % % %
РАСЧЁТ СУБСИДИЙ МНОГОДЕТНЫМ СЕМЬЯМ.
% % % % % % %
ФОНД ФИНАНСИРОВАНИЯ НАЦИОНАЛЬНЫХ ПРОЕКТОВ.
ПРОМЫШЛЕННОСТЬ
И
ТРАНСПОРТ.
% % % % % % %
ЗАДАЧА О НАСОСАХ.
% % % % % % %
ПРОКАЧКА НЕФТИ/ГАЗА ЧЕРЕЗ МАГИСТРАЛЬНЫЙ ТРУБОПРОВОД.
СЕЛЬСКОЕ ХОЗЯЙСТВО.
% % % % % % %
ЗАДАЧА ОБ УРОЖАЕ.
% % % % % % %
ЗАДАЧА ОБ ЭЛЕВАТОРХ.
НАУКА И ТЕХНИКА.
% % % % % % %
ПРОКЛАДКА ТРАНСПОРТНОГО МАРШРУТА.
БАНКИ И ФИНАНСЫ.
% % % % % % %
ВАЛЮТНАЯ КОРЗИНА.
ПРОИЗВОДСТВО.
% % % % % % %
ФОНД ЗАРАБОТНОЙ ПЛАТЫ ЗАВОДА.
% % % % % % %
РЕНТАБЕЛЬНОСТЬ ШВЕЙНОГО ПРОИЗВОДСТВА.
Большое количество схожих алгоритмов можно найти в расчётах электрических сетей и других разделах физики. Все они в один клик решаются приложением в магазине приложений
СКАЧИВАЕМ.


Сроки действия доменов и SSL-сертификатов Н А Ш И Х сайтов заканчиваются. Д Л Я п о м о щ и в их П Р О Д Л Е Н И И СКАЧИВАЙТЕ приложения в российском магазине приложений





И явился ему во сне ДЖИНН и сказал: "Вот тебе 100000 динаров! Если будешь отдавать каждую ночь такую часть этих динаров, чтобы она была больше, чем часть предыдущей но- чи, а на последнюю ночь полной луны ты отдашь всю сумму - эти динары станут твоими." Проснулся бедняк - и сделал Э Т О. Из неопубликованных сказок "Тысяча и одна ночь".
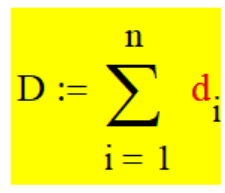
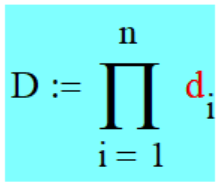
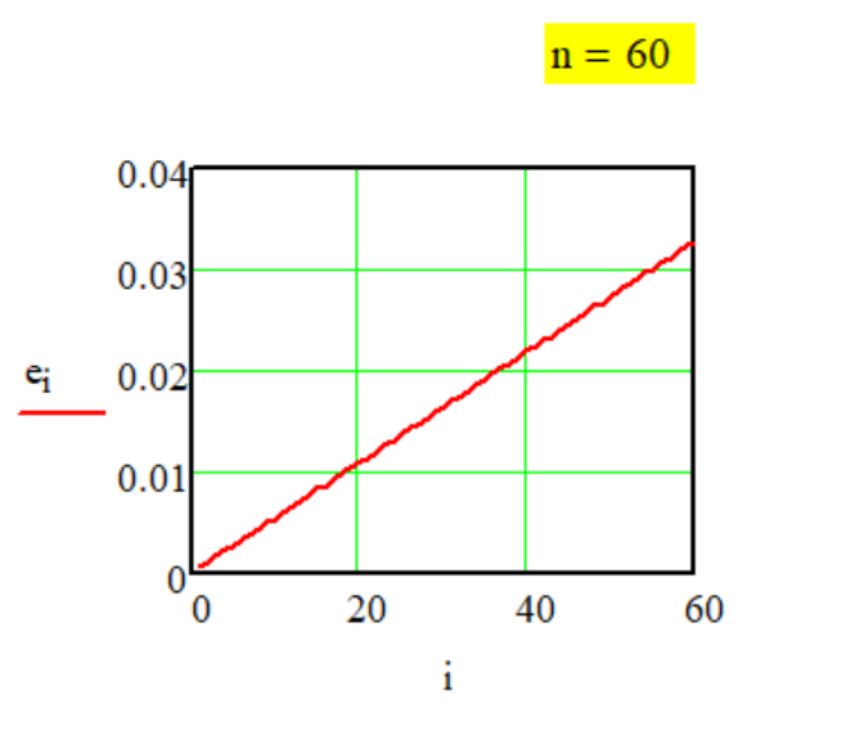
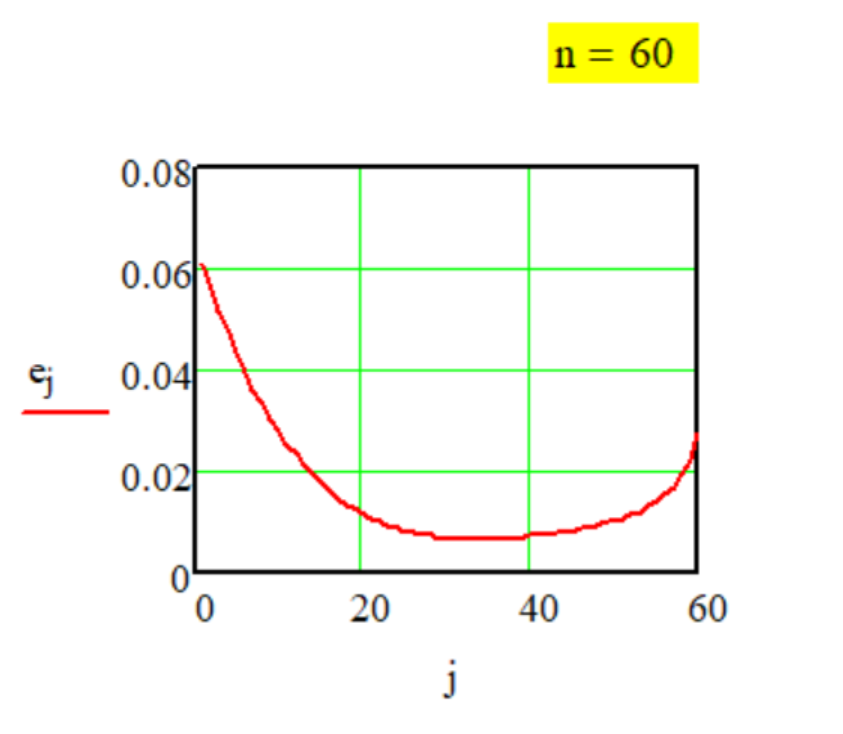
1.1. Передаточная
функция
Метода G-1-1.
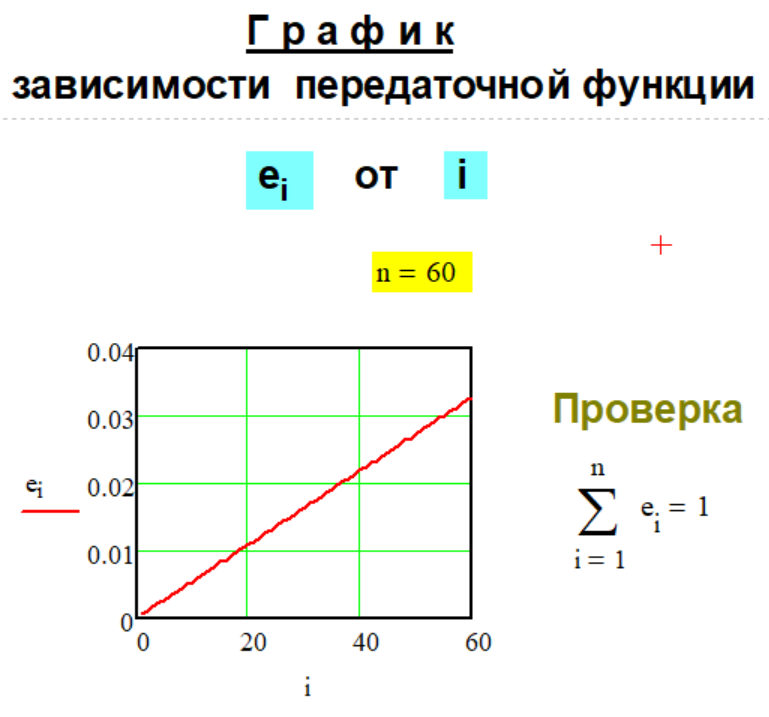
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
с л а г а е м ы х.
№№ слагаемых
декомпозиции числа
суммой.
Г Р А Ф И К
с у м м ы
с л а г а е м ы х.
№№ слагаемых
декомпозиции числа
суммой.
1.2. Передаточная
функция
Метода G-1-2.
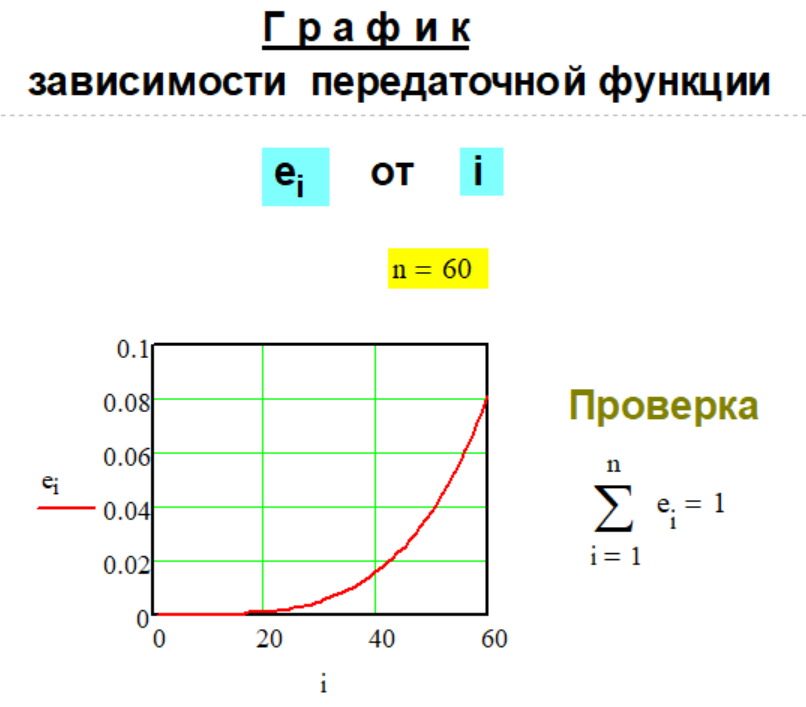
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
с л а г а е м ы х.
№№ слагаемых
декомпозиции числа
суммой.
Г Р А Ф И К
с у м м ы
с л а г а е м ы х.
№№ слагаемых
декомпозиции числа
суммой.
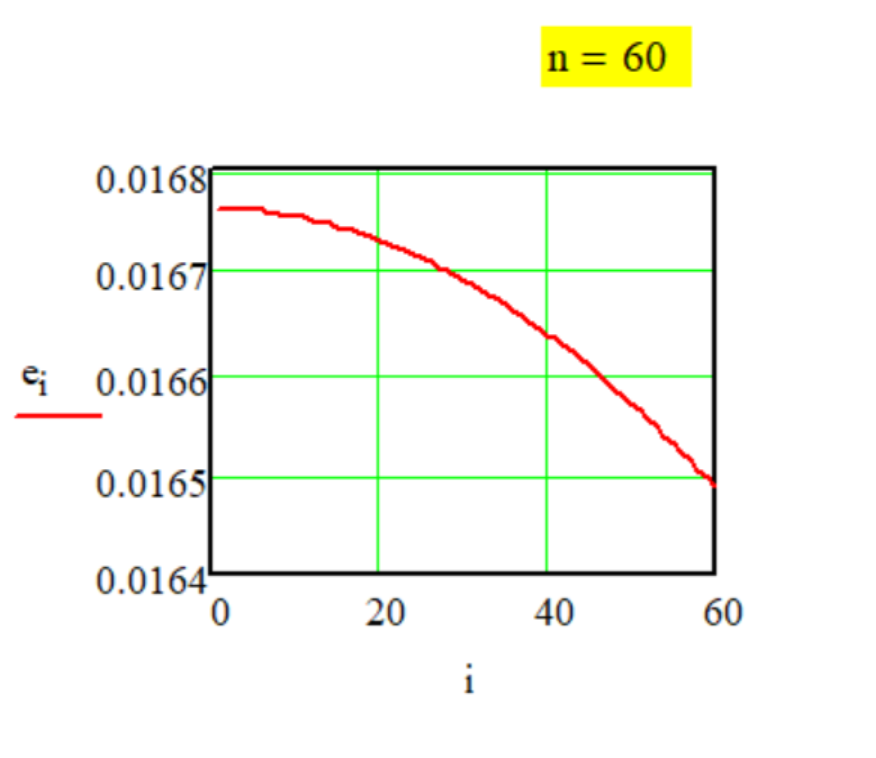
1.3. Передаточная
функция
Метода G-1-3.
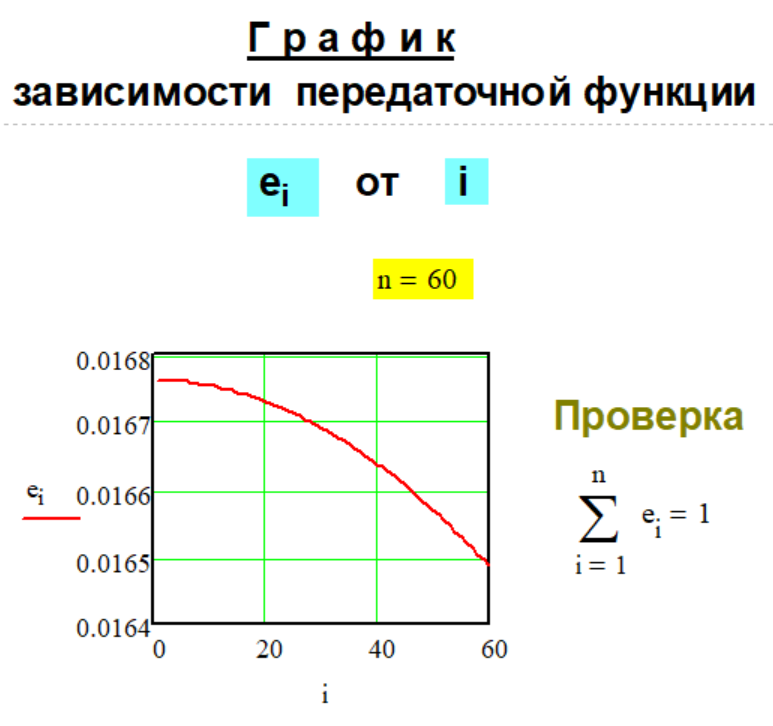
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
с л а г а е м ы х.
№№ слагаемых
декомпозиции числа
суммой.
Г Р А Ф И К
с у м м ы
с л а г а е м ы х.
№№ слагаемых
декомпозиции числа
суммой.
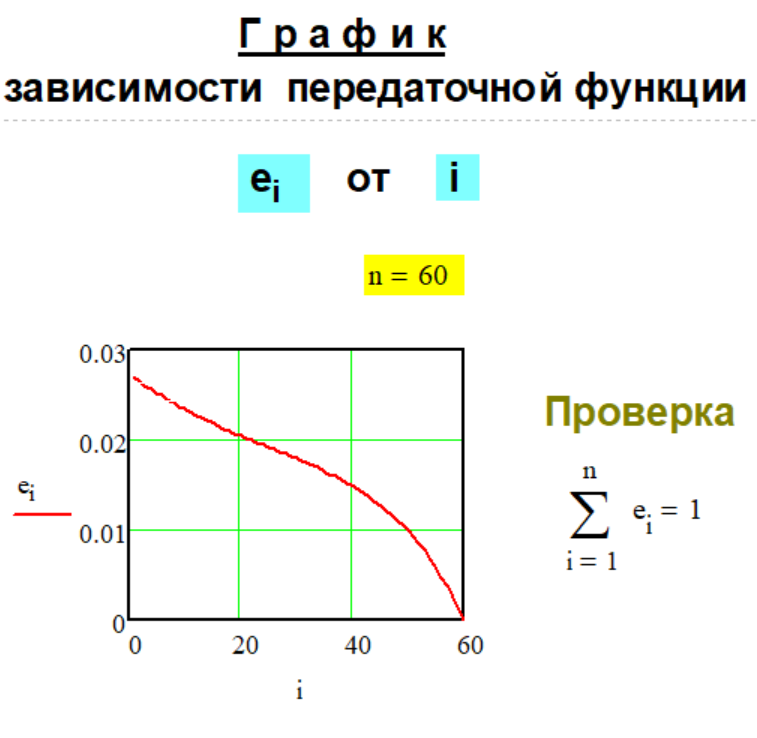
1.4. Передаточная
функция
Метода G-1-4.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
с л а г а е м ы х.
№№ слагаемых
декомпозиции числа
суммой.
Г Р А Ф И К
с у м м ы
с л а г а е м ы х.
№№ слагаемых
декомпозиции числа
суммой.
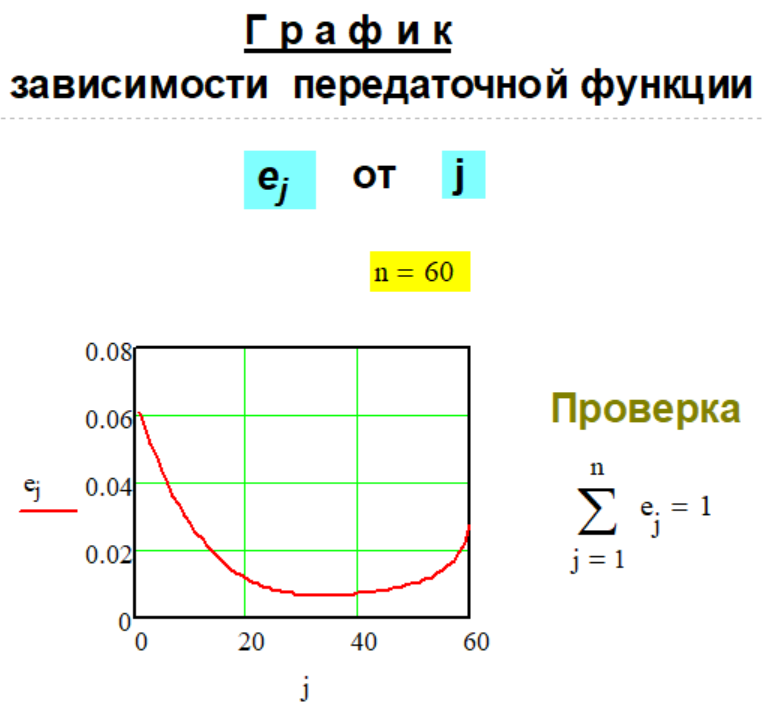
1.5. Передаточная
функция
Метода G-1-5.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
с л а г а е м ы х.
№№ слагаемых
декомпозиции числа
суммой.
Г Р А Ф И К
с у м м ы
с л а г а е м ы х.
№№ слагаемых
декомпозиции числа
суммой.
ДОПОЛНИТЕЛЬНО 33 варианта широкого спектра передаточных функций декомпозиции числа суммой можно найти в приложении российского магазина приложений

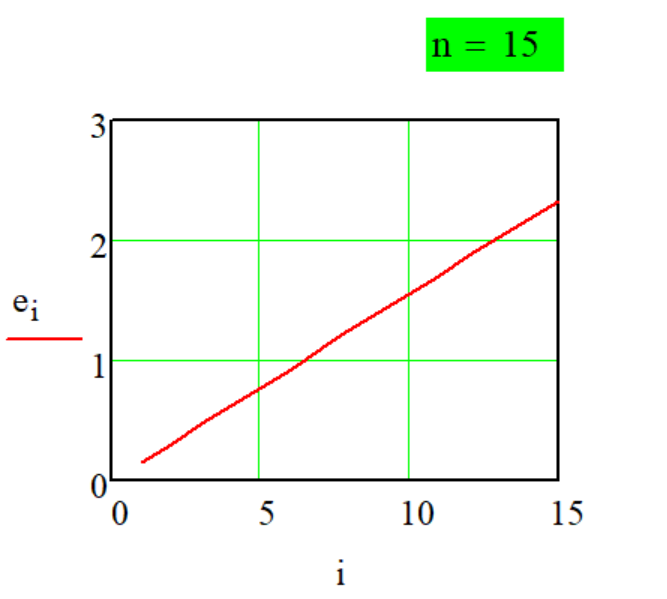
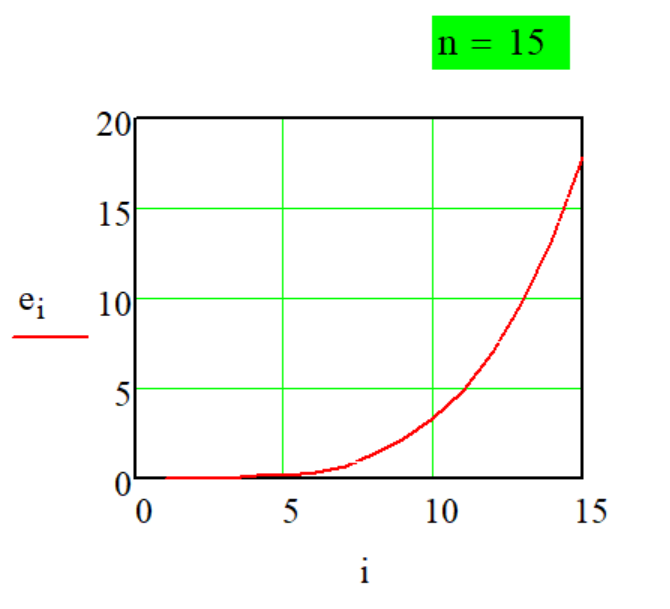
Передаточная
функция
Метода P-1-1.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
Г Р А Ф И К
п р о и з в е д е н и я
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
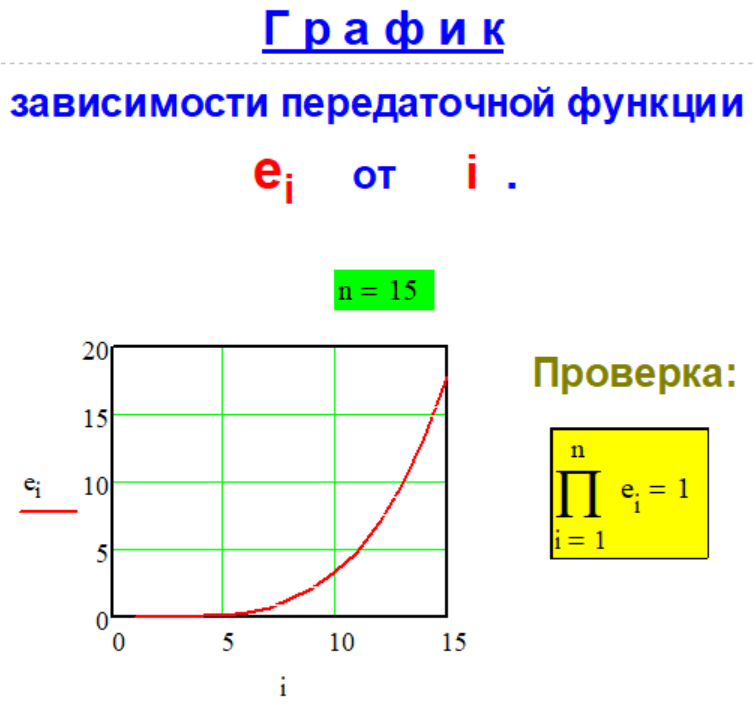
Передаточная
функция
Метода P-1-2.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
Г Р А Ф И К
п р о и з в е д е н и я
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
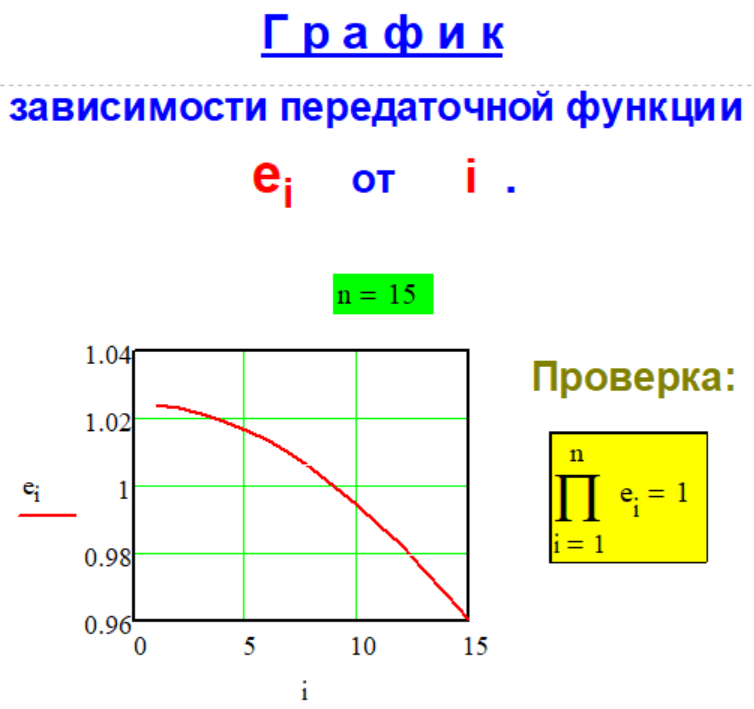
Передаточная
функция
Метода P-1-3.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
Г Р А Ф И К
п р о и з в е д е н и я
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
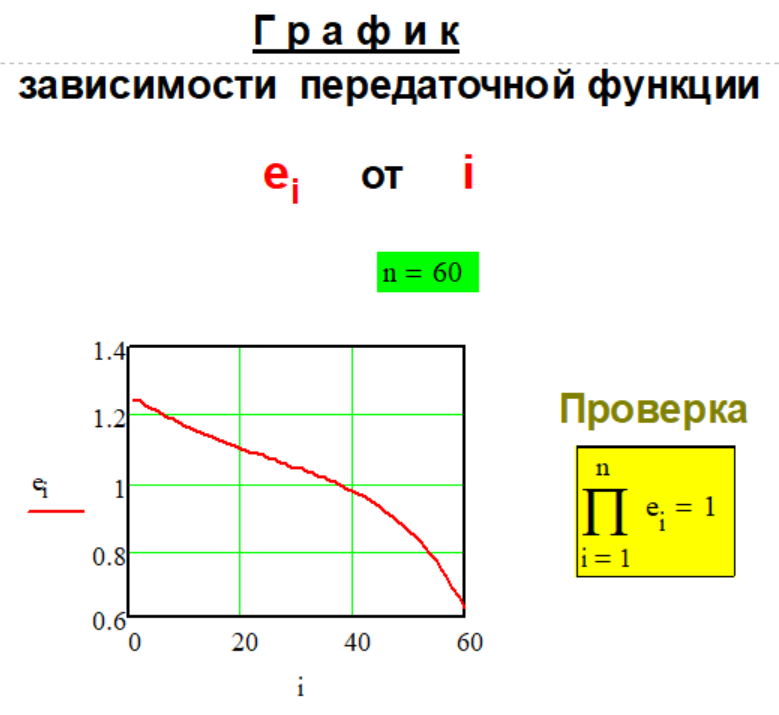
Передаточная
функция
Метода P-1-4.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
Г Р А Ф И К
п р о и з в е д е н и я
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
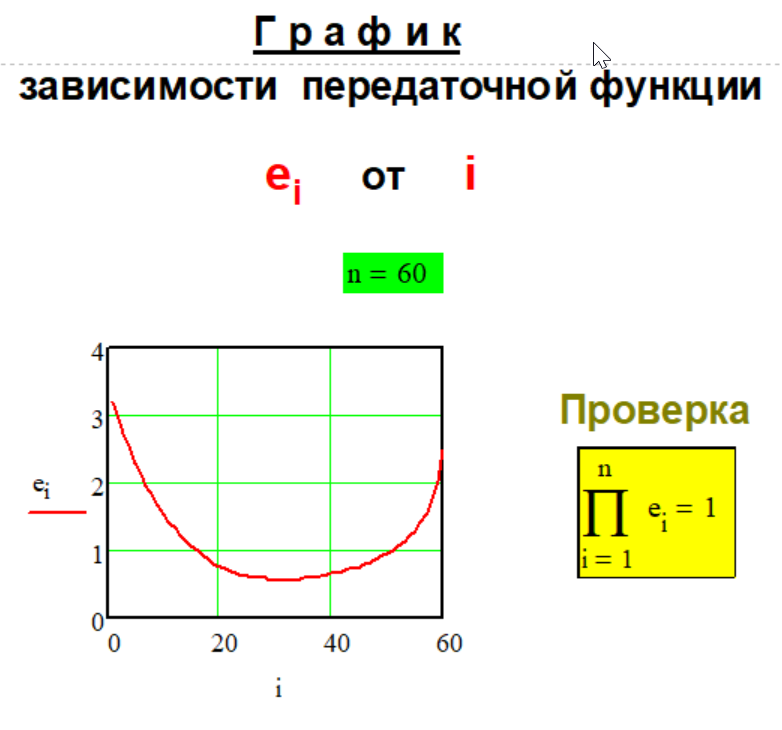
Передаточная
функция
Метода P-1-5.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
Г Р А Ф И К
п р о и з в е д е н и я
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
ДОПОЛНИТЕЛЬНО 33 варианта широкого спектра передаточных функций декомпозиции числа произведением можно найти в приложении российского магазина приложений

Метод PG-1-1.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
р а с ч ё т н ы х
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
Г Р А Ф И К
п р о и з в е д е н и я
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
Метод PG-1-2.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
р а с ч ё т н ы х
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
Г Р А Ф И К
п р о и з в е д е н и я
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
Метод PG-1-3.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
р а с ч ё т н ы х
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
Г Р А Ф И К
п р о и з в е д е н и я
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
Метод PG-1-4.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
р а с ч ё т н ы х
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
Г Р А Ф И К
п р о и з в е д е н и я
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
Метод PG-1-5.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
р а с ч ё т н ы х
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
Г Р А Ф И К
п р о и з в е д е н и я
с о м н о ж и т е л е й.
№№ сомножителей
декомпозиции числа
произведением.
ДОПОЛНИТЕЛЬНО 33 варианта широкого спектра методов пересчёта можно найти в приложении российского магазина приложений


Сроки действия доменов и SSL-сертификатов Н А Ш И Х сайтов заканчиваются. Д Л Я п о м о щ и в их П Р О Д Л Е Н И И СКАЧИВАЙТЕ приложения в российском магазине приложений








И явился ему во сне ДЖИНН и сказал: "Вот тебе 100000 динаров! Если будешь отдавать каждую ночь такую часть этих динаров, чтобы она была больше, чем часть предыдущей но- чи, а на последнюю ночь полной луны ты отдашь всю сумму - эти динары станут твоими." Проснулся бедняк - и сделал Э Т О. Из неопубликованных сказок "Тысяча и одна ночь".
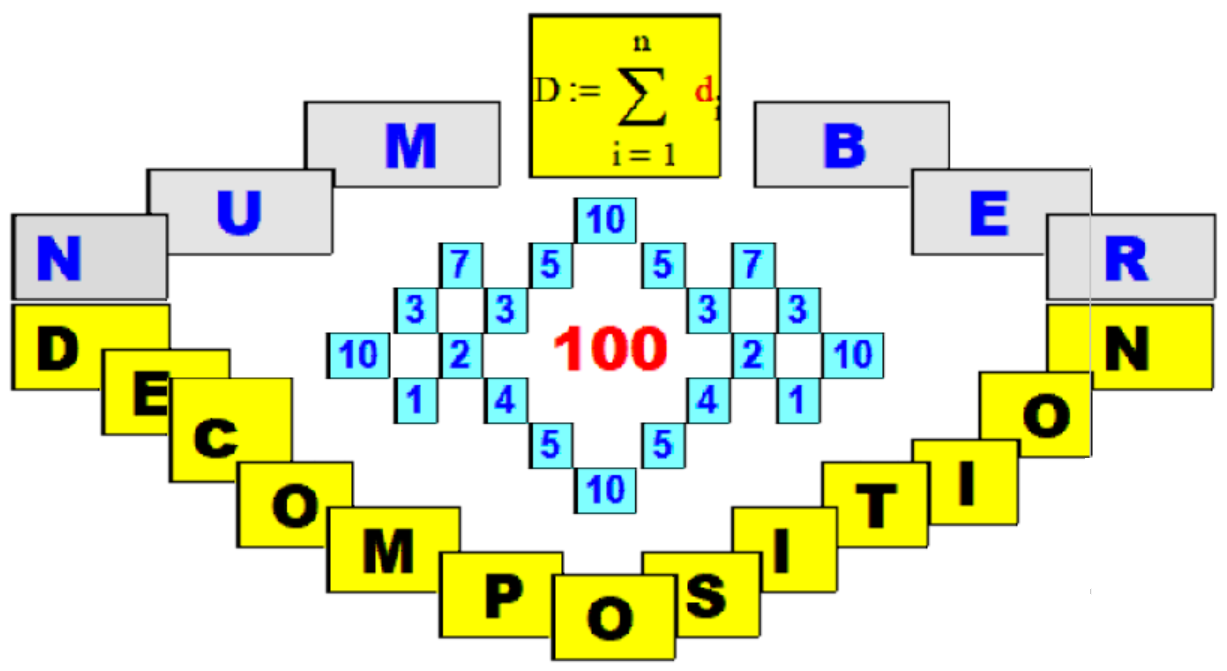
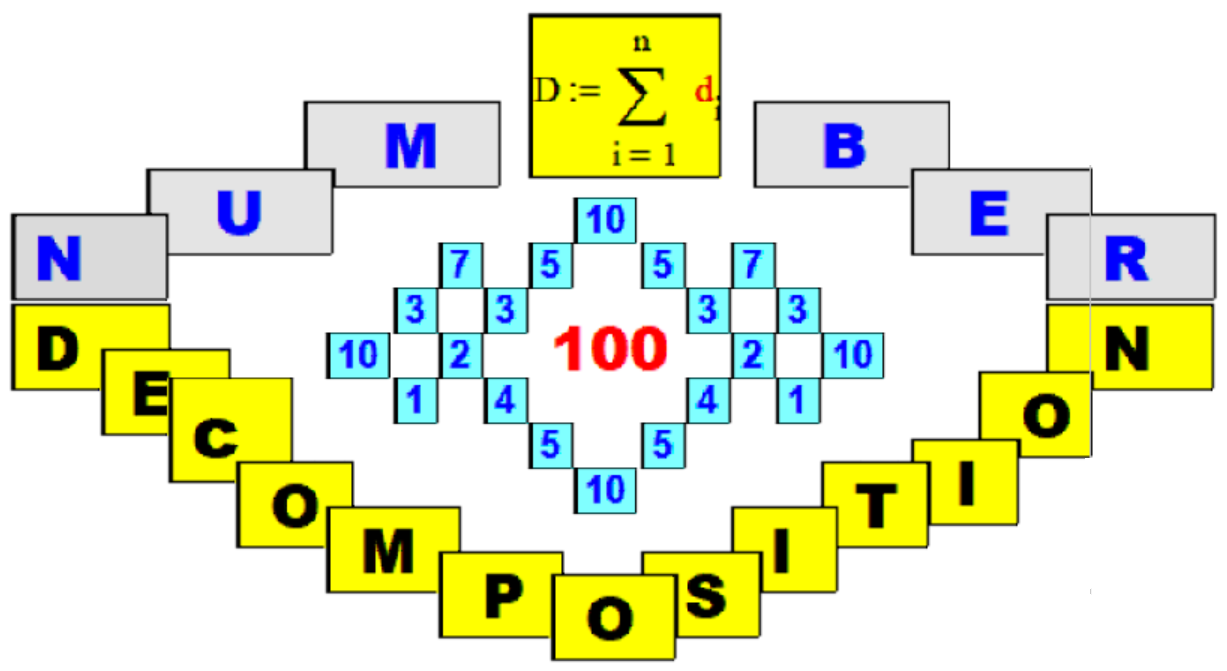
1.Вводим исходное число D , подлежащее декомпозиции. 2.Вводим цену деления шкалы времени Δt , (шаг по времени). 3.После клика на форме РАСЧЁТ заполняем окно ввода ординат графика прототипа ВАШЕЙ передаточной функции (число ординат ограничено n=3 ). "Работает" область ввода отрицательных значений ординат.После подтверждения ввода исходных данных ординат про- тотипа передаточной функции - расчёт выполняется автоматически. 4.Изучаем полученные результаты и графики ВАШЕГО расчёта. 5.Для повторных выполнений расчётов- ОБНОВИТЕ РАСЧЁТ по кнопке

ПРИМЕЧАНИЕ: Р А С Ч Ё Т Ы при n > 3 перенесёны в
В А Ш МЕТОД - ЭТО ЛЕГКО!
ДЕКОМПОЗИЦИЯ
ЧИСЛА
СУММОЙ.
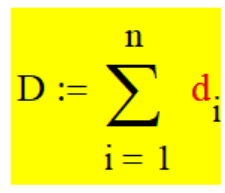
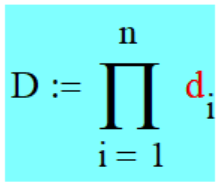
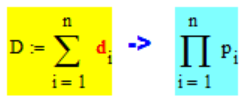
ДЕКОМПОЗИЦИЯ
ЧИСЛА
РЯДОМ ФУРЬЕ.
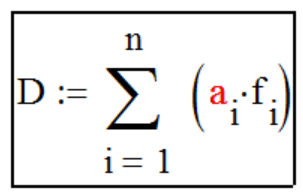
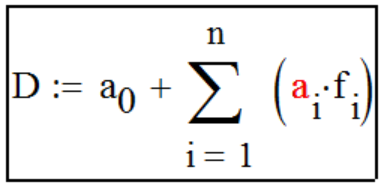
Р А С Ч Ё Т
декомпозиции
числа
суммой.
ПРИ ВВОДЕ: С У М М А ординат прототипа передаточной функции декомпозиции числа fi НЕ РАВНА НУЛЮ.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
п р о т о т и п а
п е р е д а т о ч н о й
ф у н к ц и и.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
с у м м ы
с л а г а е м ы х.
Расчётные
интервалы времени,
ti .
ДОПОЛНИТЕЛЬНО
ВАШИ
варианты
( при n >3 )
задания
прототипа
передаточной
функции
декомпозиции
числа суммой
можно
РЕАЛИЗОВАТЬ
в
приложении
российского
магазина
приложений


Р А С Ч Ё Т
декомпозиции
числа
произведением.
ПРИ ВВОДЕ: Ординаты прототипа передаточной функции декомпозиции числа fi НЕ РАВНЫ НУЛЮ.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
п р о т о т и п а
п е р е д а т о ч н о й
ф у н к ц и и.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
с о м н о ж и т е л е й.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
п р о и з в е д е н и я
с о м н о ж и т е л е й.
Расчётные
интервалы времени,
ti .
ДОПОЛНИТЕЛЬНО
ВАШИ
варианты
( при n >3 )
задания
прототипа
передаточной
функции
декомпозиции
числа
произведнием
можно
РЕАЛИЗОВАТЬ
в
приложении
российского
магазина
приложений


П Е Р Е С Ч Ё Т
декомпозиции
числа
произведением
от
декомпозиции суммой.
ПРИ ВВОДЕ: Ординаты прототипа передаточной функции декомпозиции числа fi НЕ РАВНЫ НУЛЮ.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
п р о т о т и п а
п е р е д а т о ч н о й
ф у н к ц и и.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
с о м н о ж и т е л е й.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
п р о и з в е д е н и я
с о м н о ж и т е л е й.
Расчётные
интервалы времени,
ti .
ДОПОЛНИТЕЛЬНО
ВАШИ
варианты
( при n >3 )
задания
прототипа
передаточной
функции
метода пересчёта
можно
РЕАЛИЗОВАТЬ
в
приложении
российского
магазина
приложений


Р А С Ч Ё Т
декомпозиции
числа
рядом Фурье
без
свободного члена.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
ф у н к ц и и
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
к о э ф ф и ц и е н т о в
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
с у м м ы
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
ДОПОЛНИТЕЛЬНО
ВАШИ
варианты
( при n >3 )
задания
прототипа
передаточной
функции
метода Фурье
без
свободного члена
можно
РЕАЛИЗОВАТЬ
в
приложении
российского
магазина
приложений


Р А С Ч Ё Т
декомпозиции
числа
рядом Фурье
со
свободным членом.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
ф у н к ц и и
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
к о э ф ф и ц и е н т о в
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
с у м м ы
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
ДОПОЛНИТЕЛЬНО
ВАШИ
варианты
( при n >3 )
задания
прототипа
передаточной
функции
метода Фурье
со
свободным членом
можно
РЕАЛИЗОВАТЬ
в
приложении
российского
магазина
приложений




Сроки действия доменов и SSL-сертификатов Н А Ш И Х сайтов заканчиваются. Д Л Я п о м о щ и в их П Р О Д Л Е Н И И СКАЧИВАЙТЕ приложения в российском магазине приложений








И явился ему во сне ДЖИНН и сказал: "Вот тебе 100000 динаров! Если будешь отдавать каждую ночь такую часть этих динаров, чтобы она была больше, чем часть предыдущей но- чи, а на последнюю ночь полной луны ты отдашь всю сумму - эти динары станут твоими." Проснулся бедняк - и сделал Э Т О. Из неопубликованных сказок "Тысяча и одна ночь".
NEW METHODS of the NUMBER DECOMPOSITION.
НОВЫЕ МЕТОДЫ РАСЧЁТА ДЕКОМПОЗИЦИИ ЧИСЛА.
В А Ш МЕТОД - ЭТО ЛЕГКО!
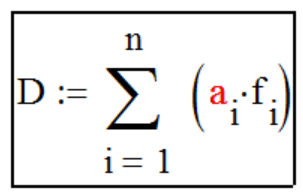
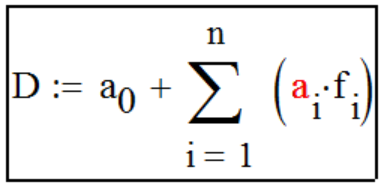
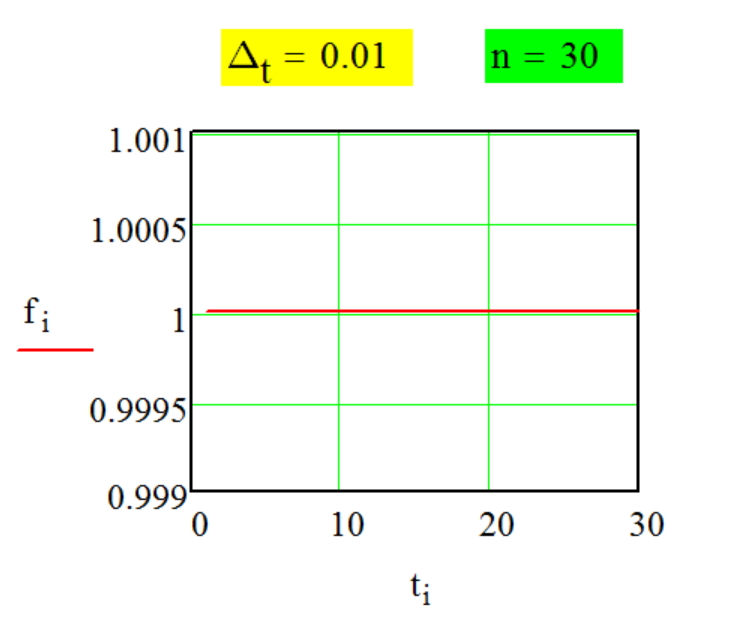




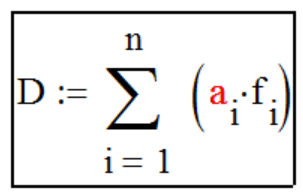
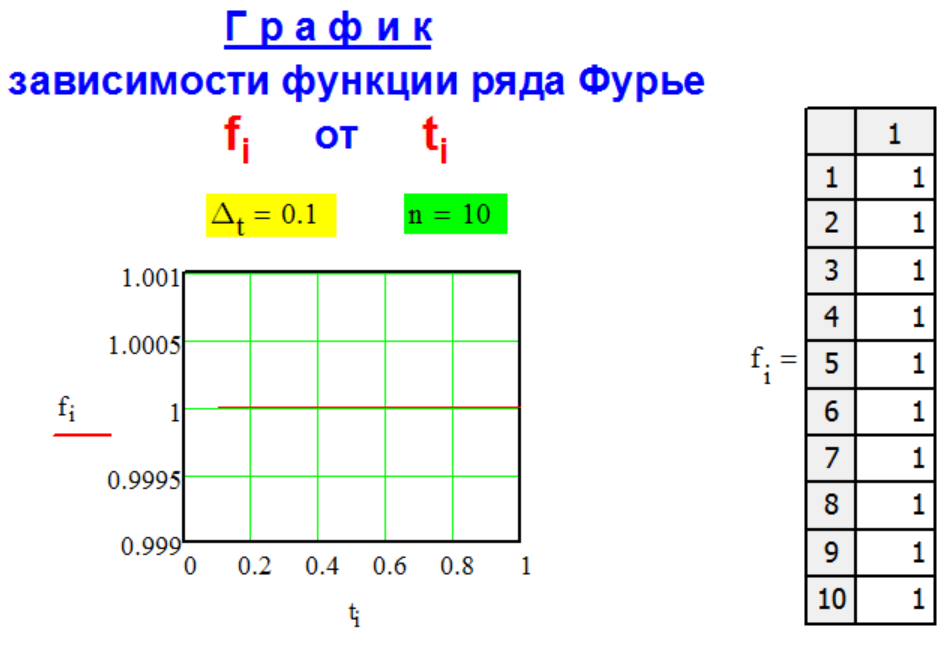
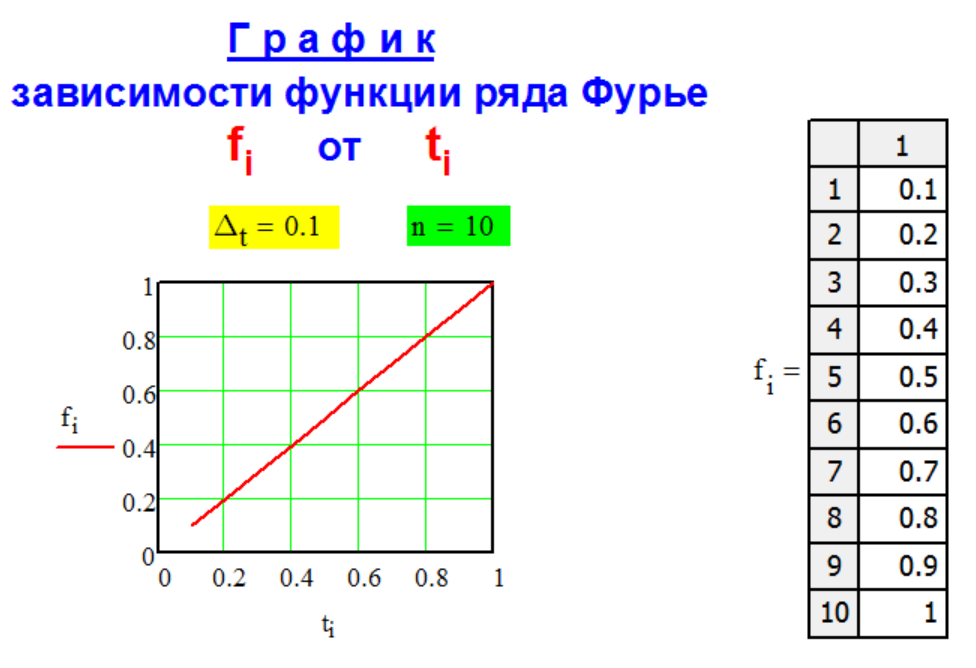
Вид
образующей функции
f[i]
ряда Фурье
f[i] = ti/ti,
где
ti - моменты времени
наблюдений;
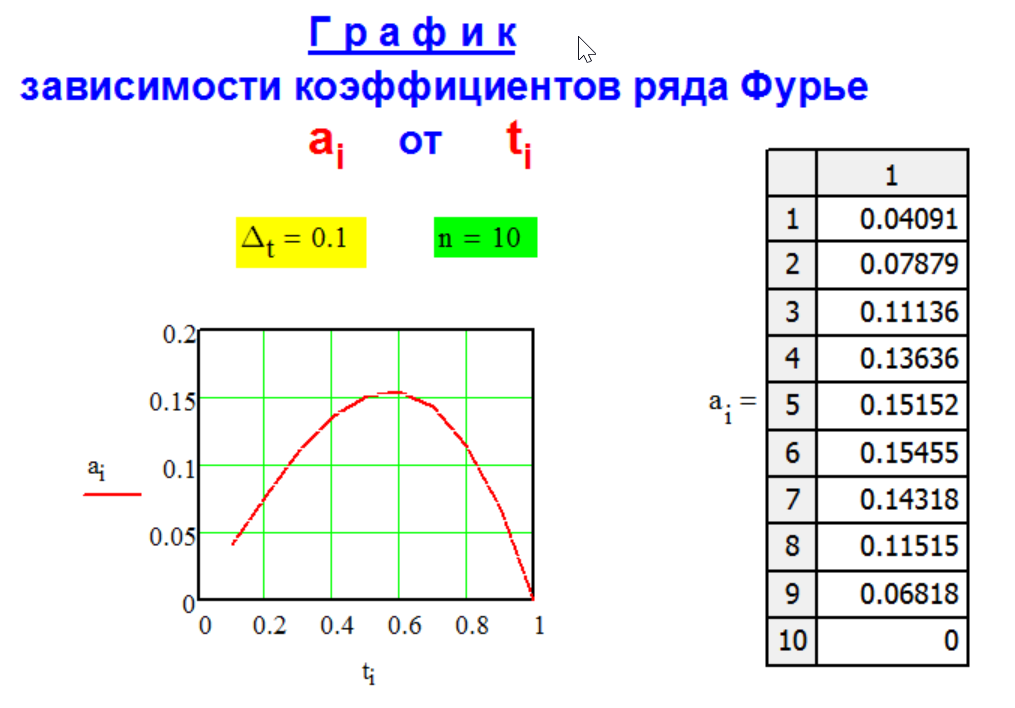
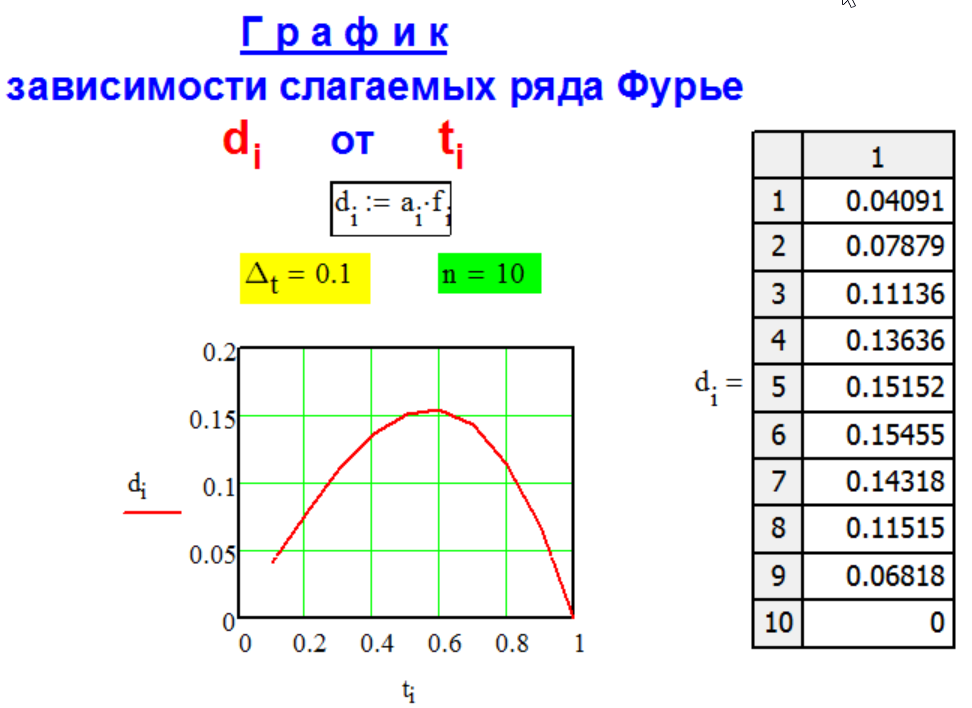
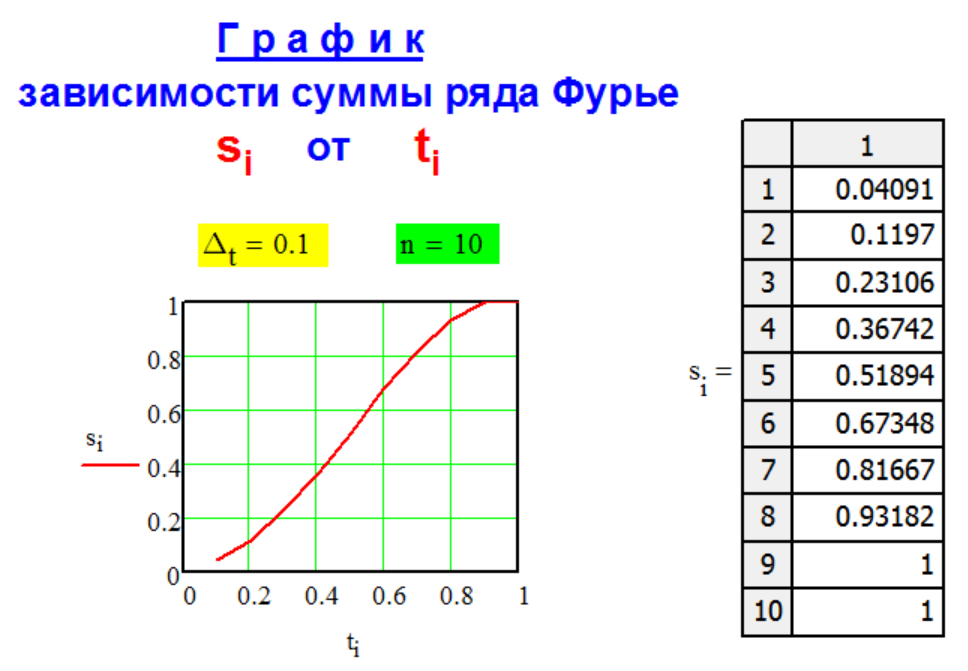
Метод FG-1-1
декомпозиции
числа
рядом Фурье.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
ф у н к ц и и
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
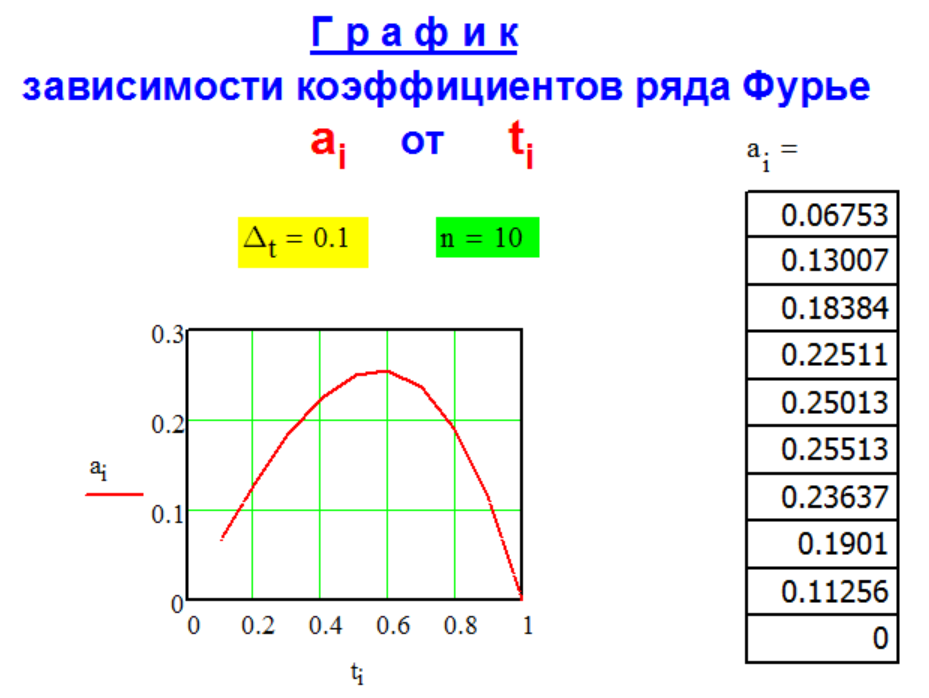
Г Р А Ф И К
р а с ч ё т н ы х
к о э ф ф и ц и е н т о в
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
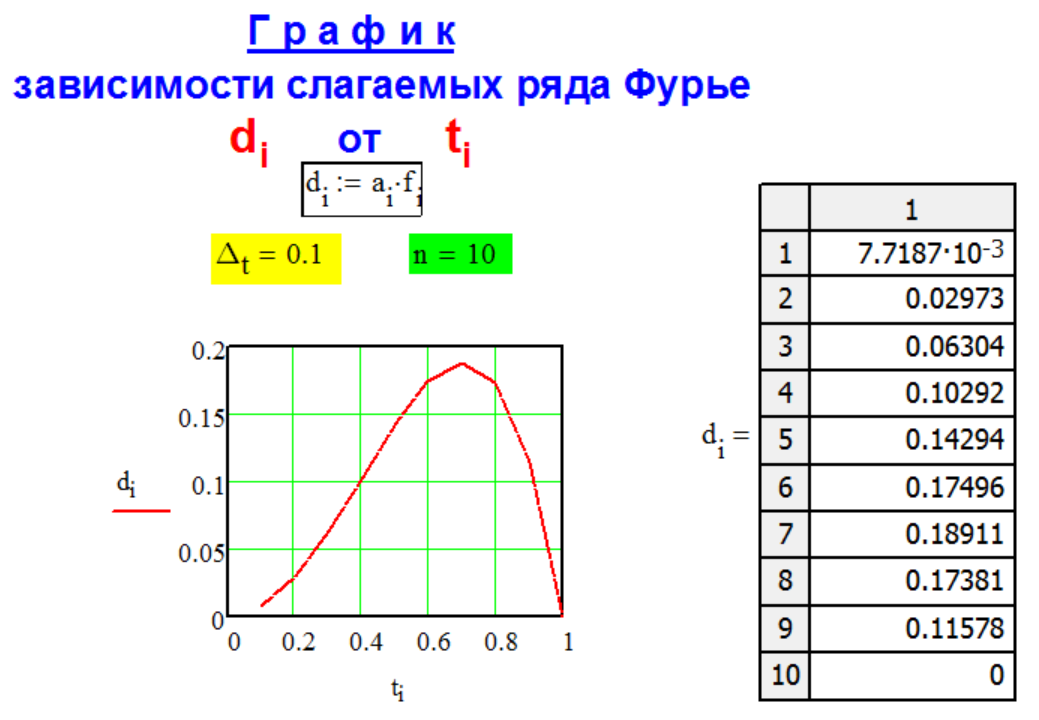
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
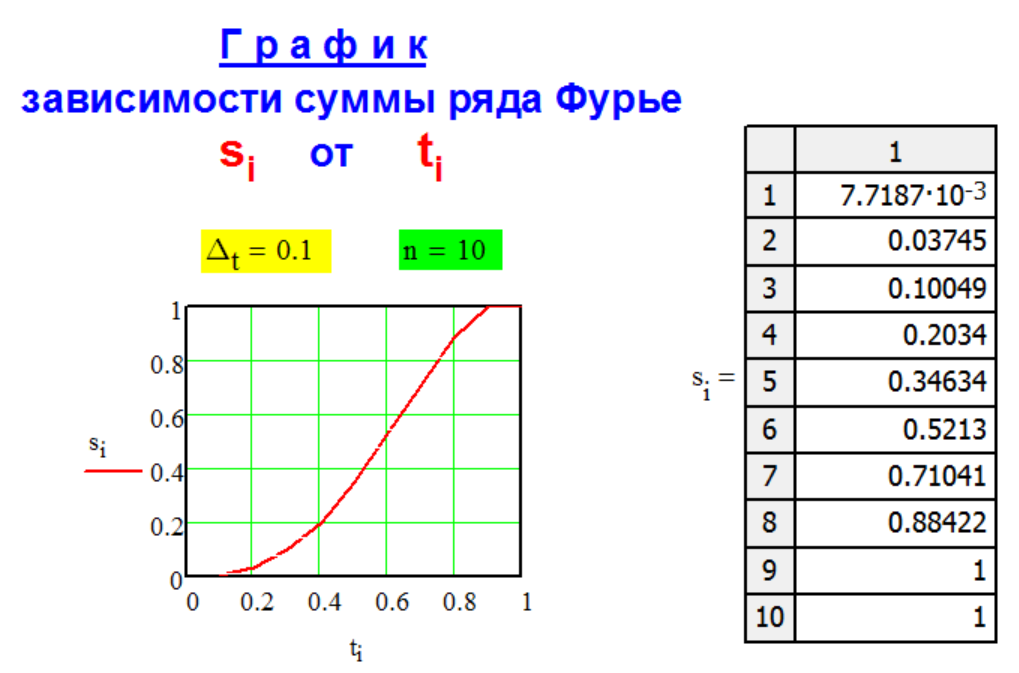
Г Р А Ф И К
с у м м ы
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
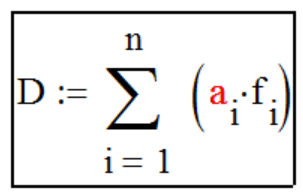
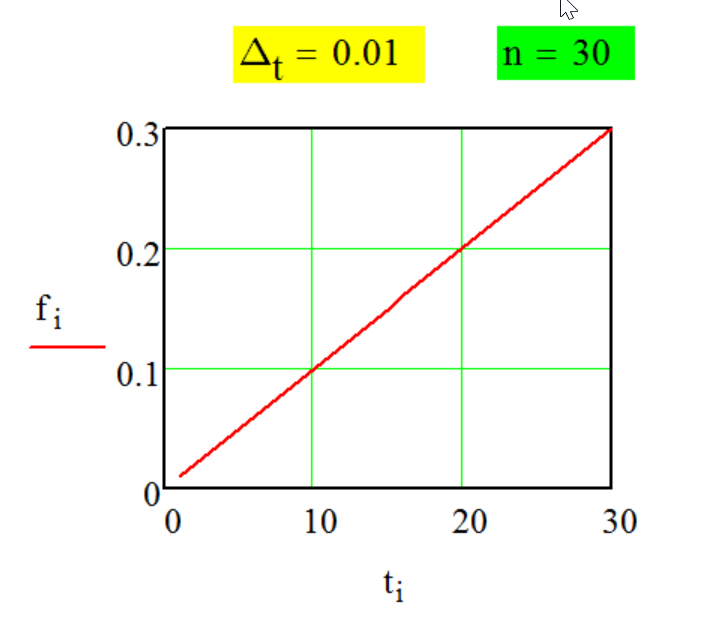
Вид
образующей функции
f[i]
ряда Фурье
f[i] = ti,
где
ti - моменты времени
наблюдений;
ti = Δt * i ;
Δt - шаг по времени.
Метод FG-1-2
декомпозиции
числа
рядом Фурье.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
ф у н к ц и и
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
к о э ф ф и ц и е н т о в
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
с у м м ы
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
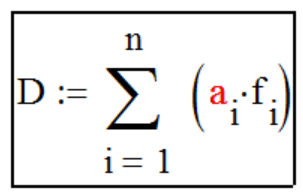
Вид
образующей функции
f[i]
ряда Фурье
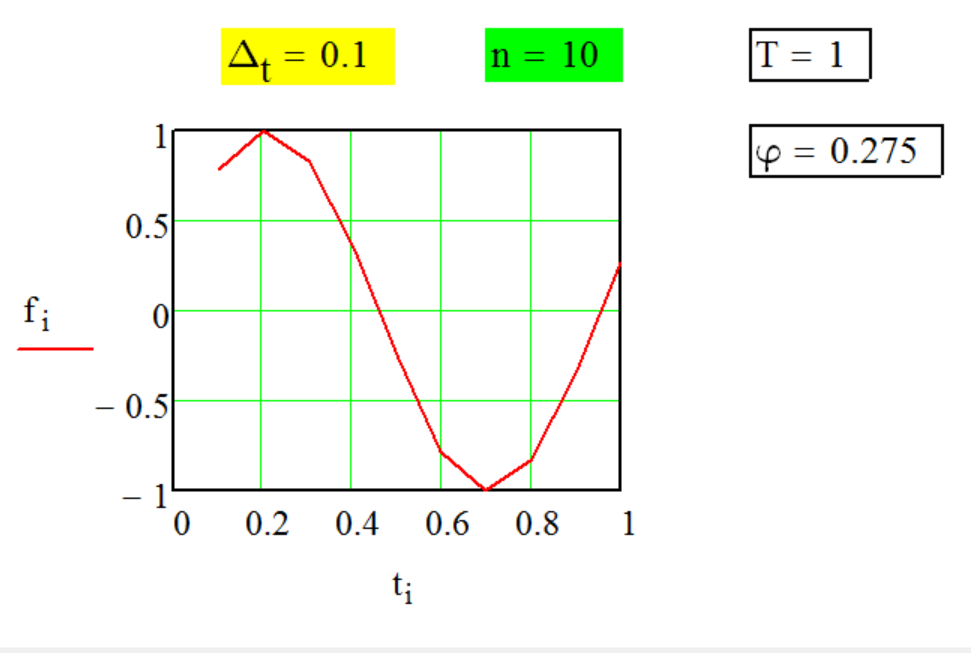
f[i] = sin(ω * ti + φ),
где
ω - частота;
ω = 2 * π / Τ
Τ - период;
φ - фаза;
ti - моменты времени
наблюдений;
ti = Δt * i ;
Δt - шаг по времени.
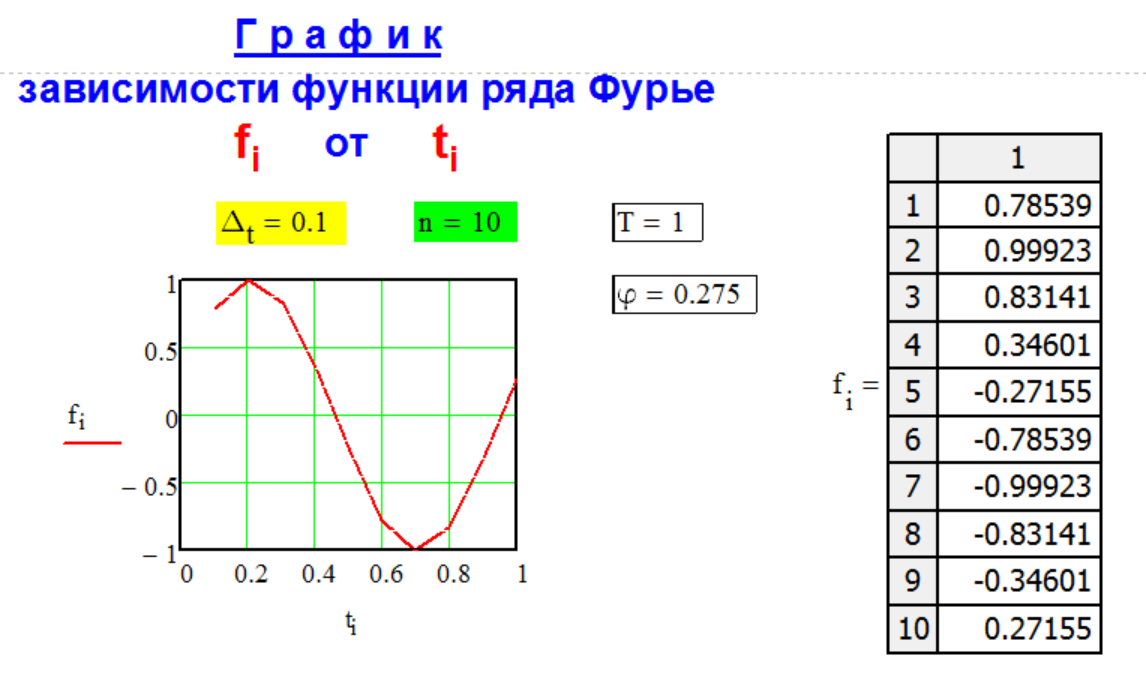

Метод FG-1-3
декомпозиции
числа
рядом Фурье.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
ф у н к ц и и
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
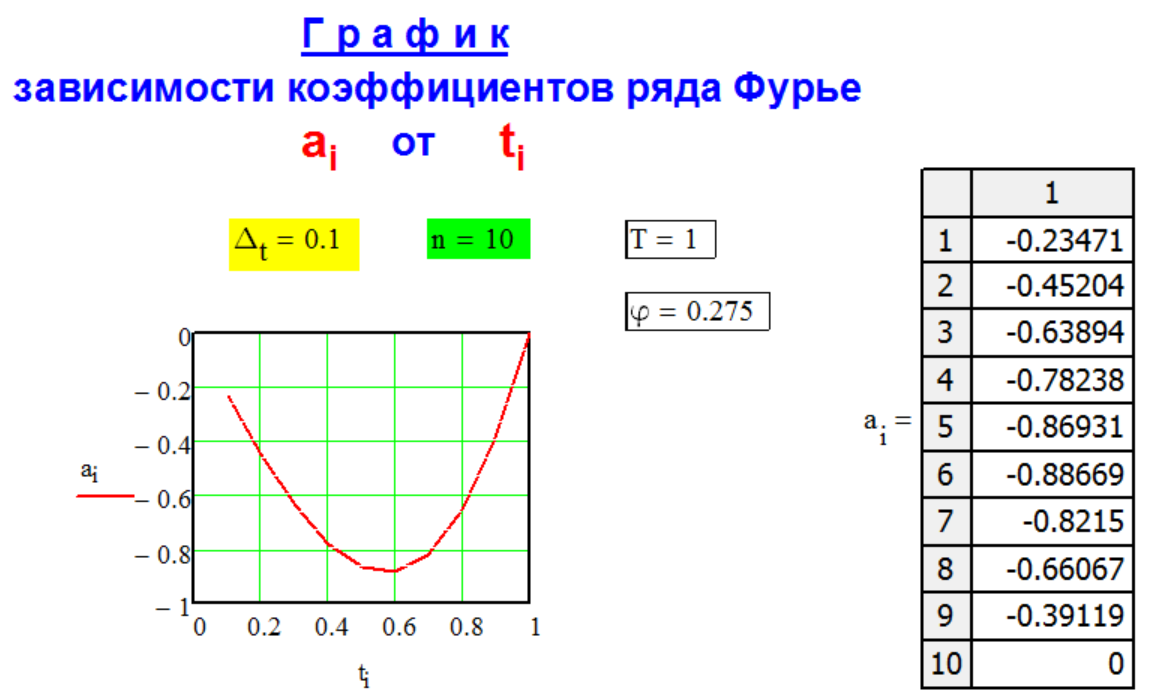
Г Р А Ф И К
р а с ч ё т н ы х
к о э ф ф и ц и е н т о в
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
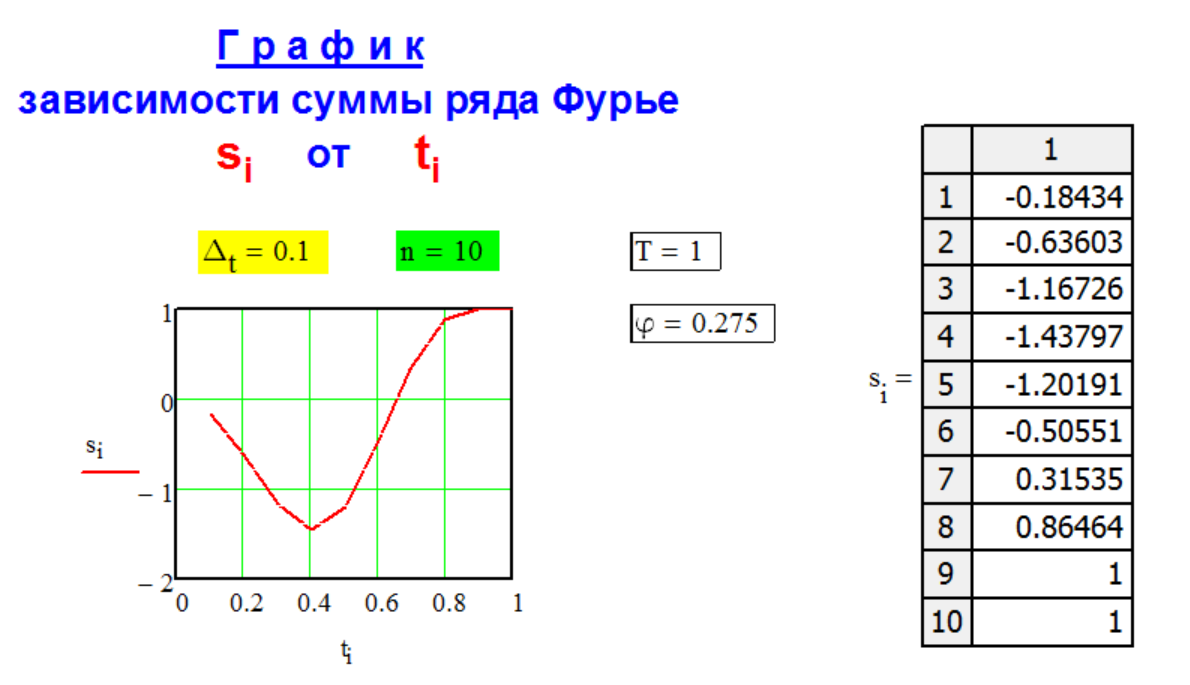
Г Р А Ф И К
с у м м ы
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
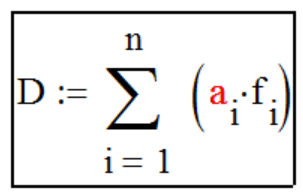
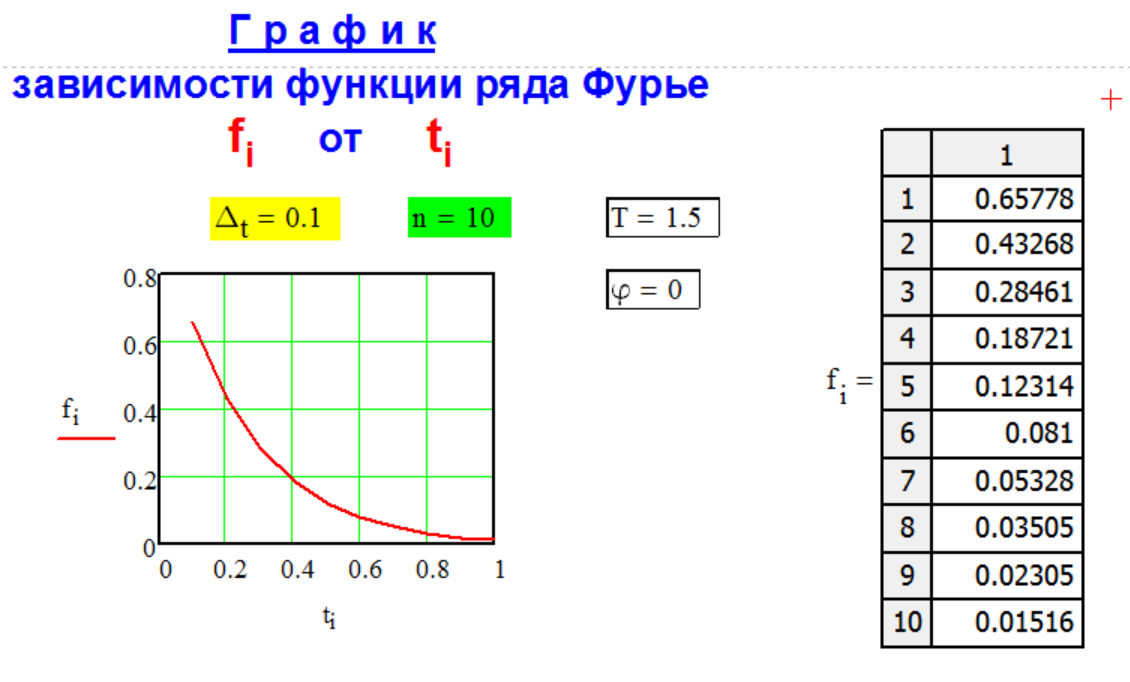
Вид
образующей функции
f[i]
ряда Фурье
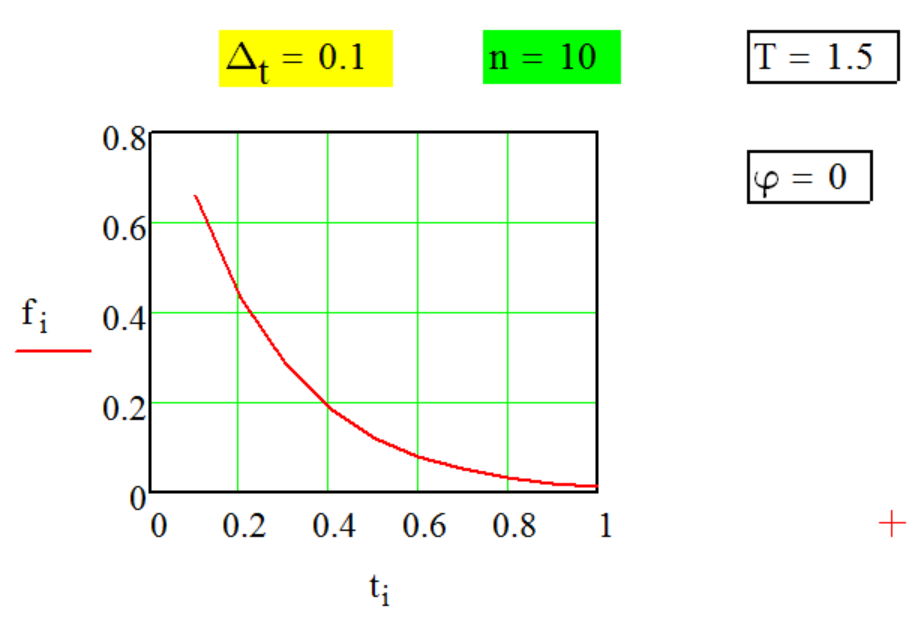
f[i] = exp[-(ω * ti + φ)] ,
где
ω - частота;
ω = 2 * π / Τ
Τ - период;
φ - фаза;
ti - моменты времени
наблюдений;
ti = Δt * i ;
Δt - шаг по времени.

Метод FG-1-4
декомпозиции
числа
рядом Фурье.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
ф у н к ц и и
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
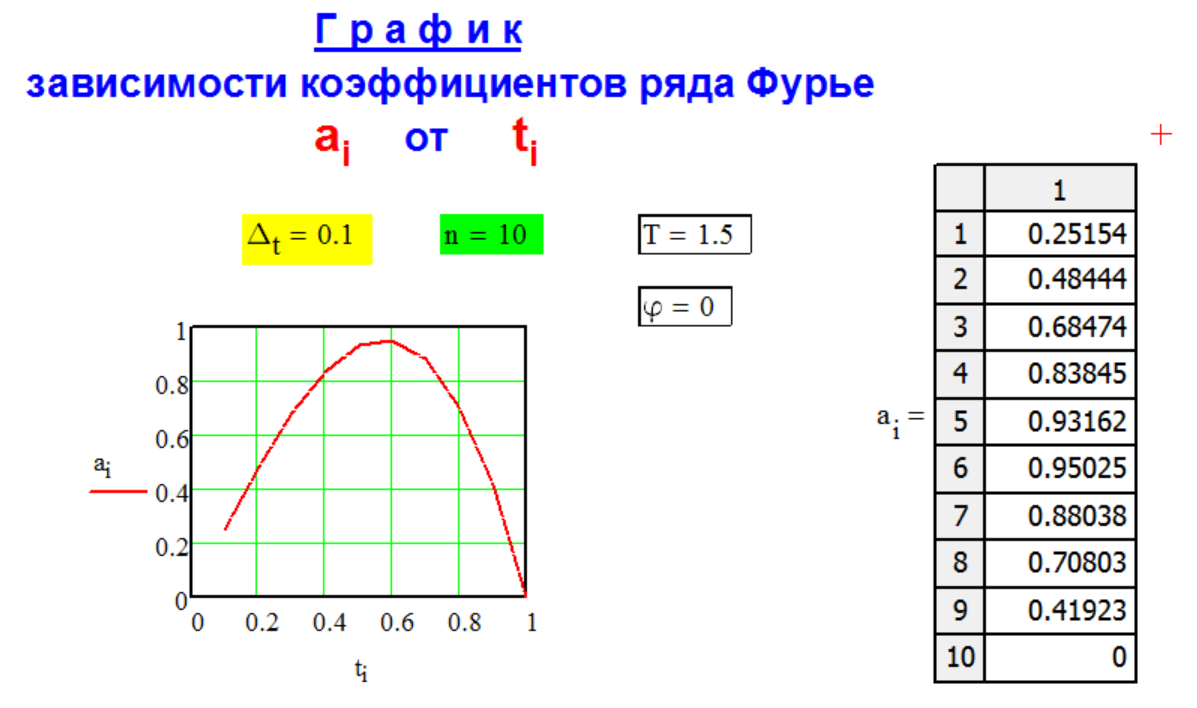
Г Р А Ф И К
р а с ч ё т н ы х
к о э ф ф и ц и е н т о в
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
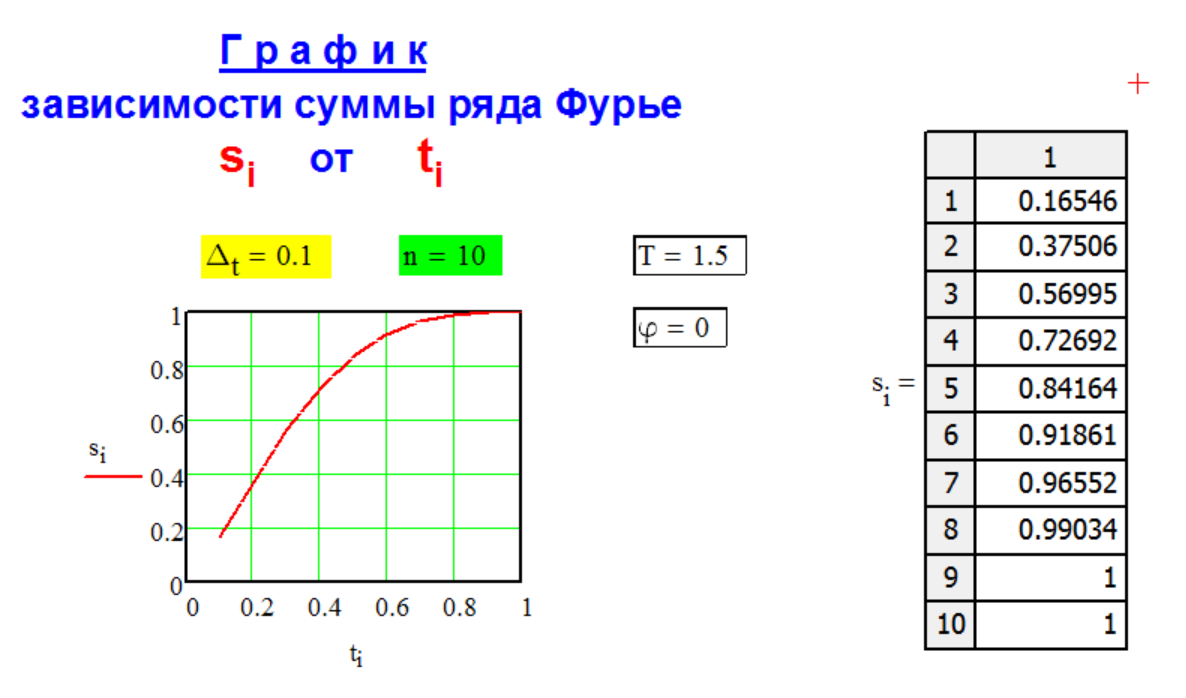
Г Р А Ф И К
с у м м ы
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
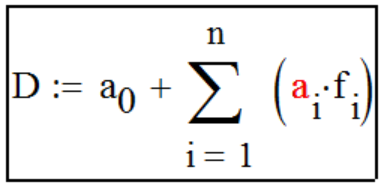
Вид
образующей функции
f[i]
ряда Фурье
f[i] = ti/ti,
где
ti - моменты времени
наблюдений;


Метод CFG-1-1
декомпозиции
числа
рядом Фурье
со
свободным членом.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
ф у н к ц и и
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
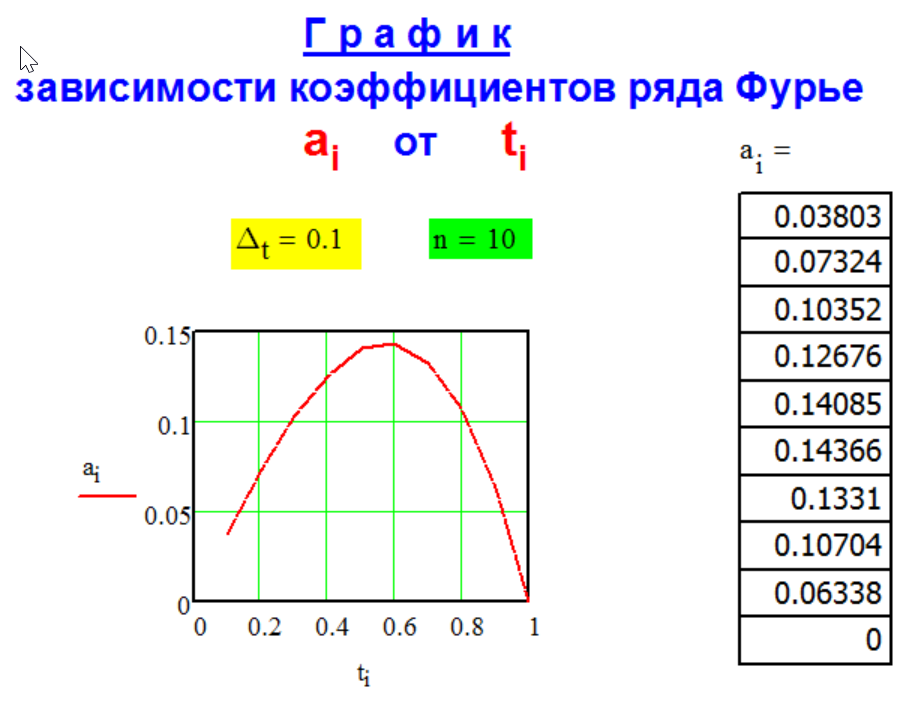
Г Р А Ф И К
р а с ч ё т н ы х
к о э ф ф и ц и е н т о в
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
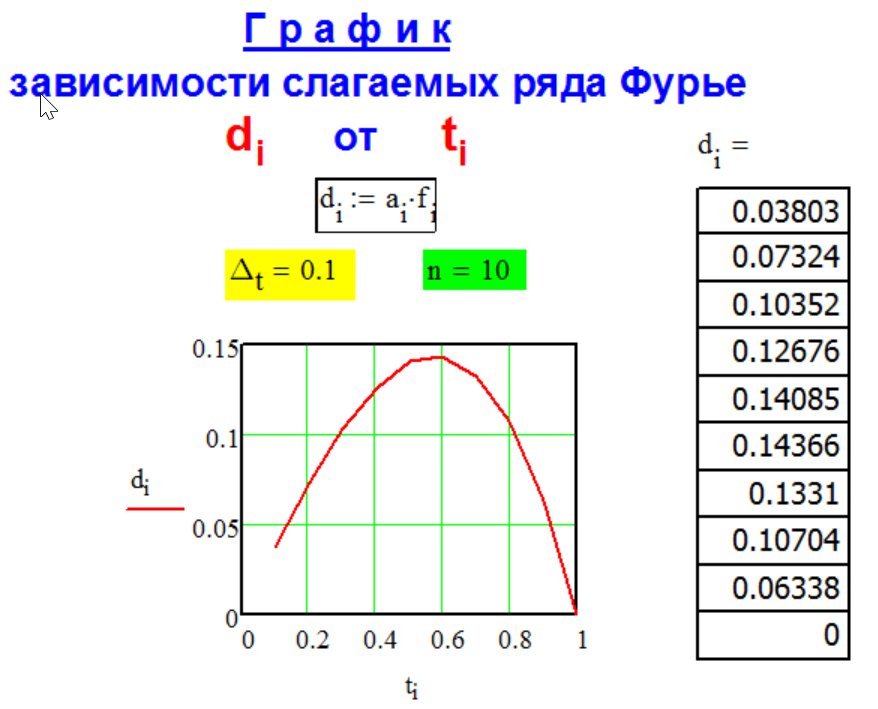
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
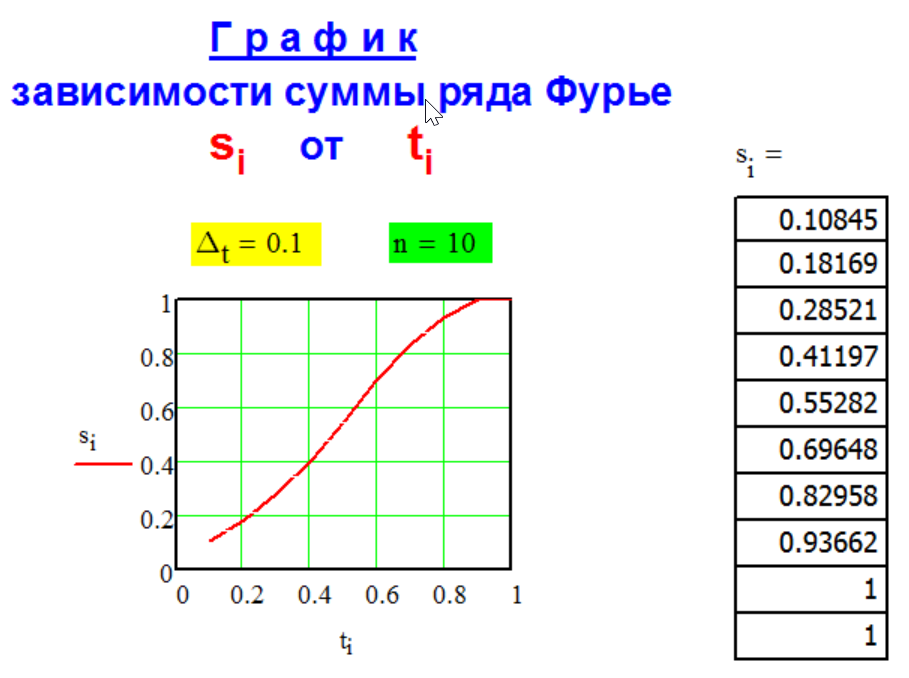
Г Р А Ф И К
с у м м ы
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
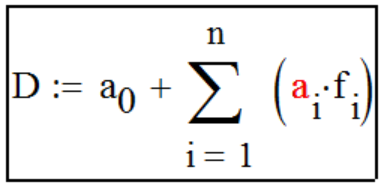
Вид
образующей функции
f[i]
ряда Фурье
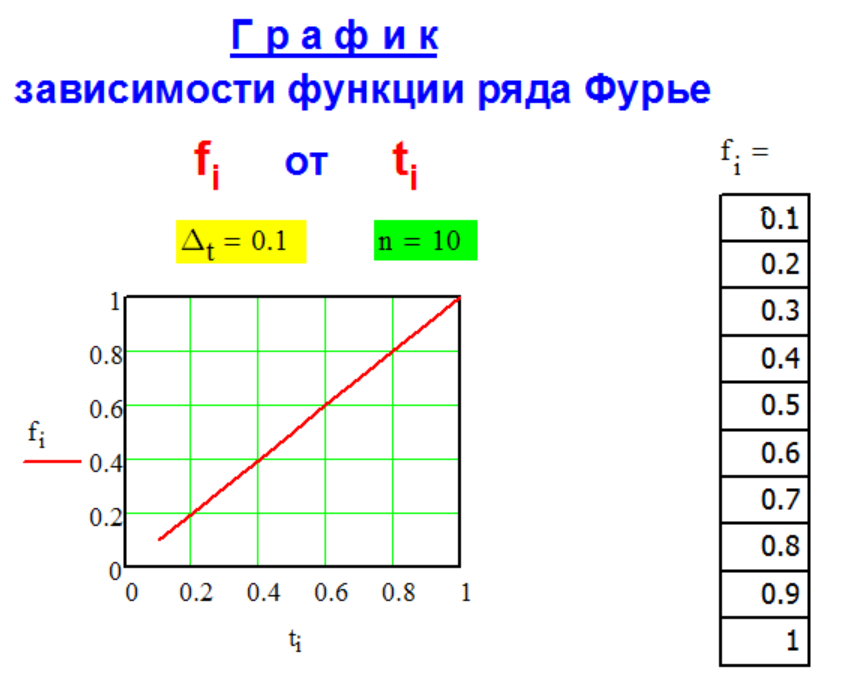
f[i] = ti,
где
ti - моменты времени
наблюдений;
ti = Δt * i ;
Δt - шаг по времени.


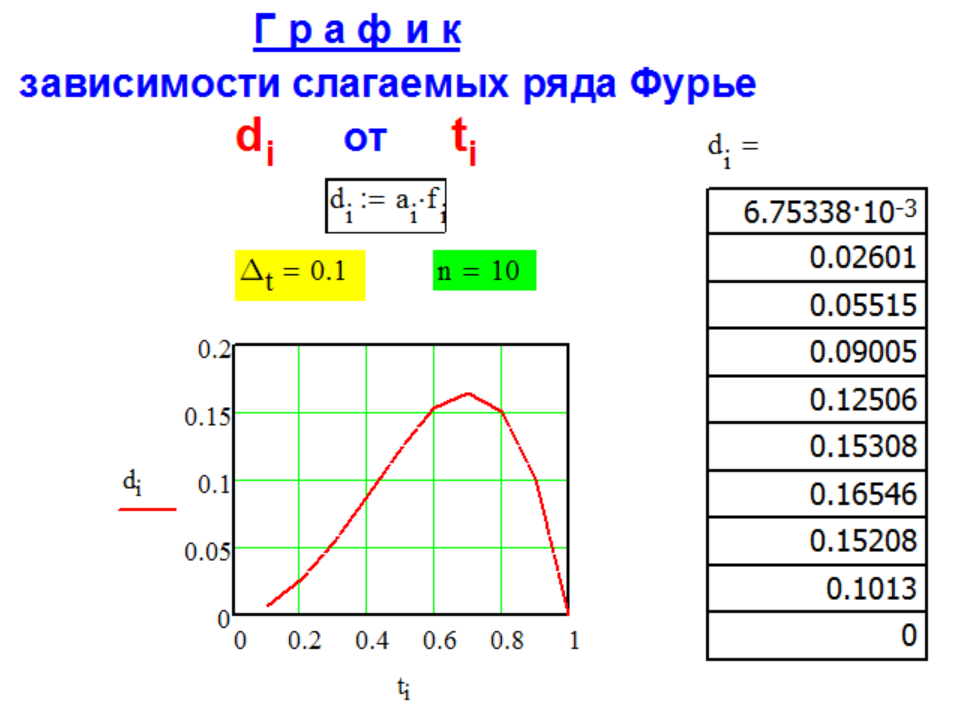
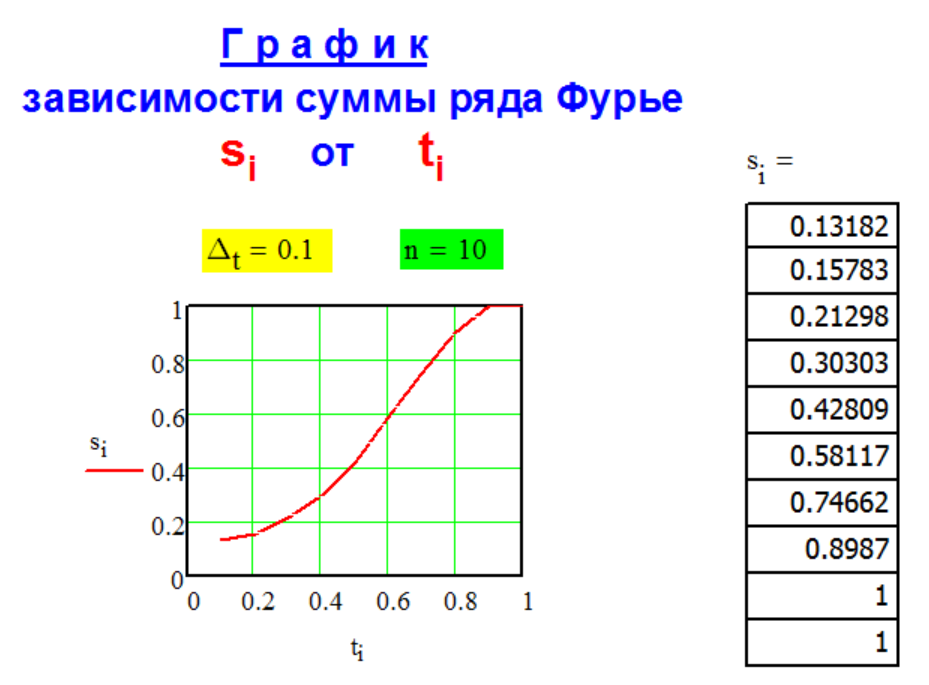
Метод CFG-1-2
декомпозиции
числа
рядом Фурье
со
свободным членом.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
ф у н к ц и и
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
к о э ф ф и ц и е н т о в
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
с у м м ы
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
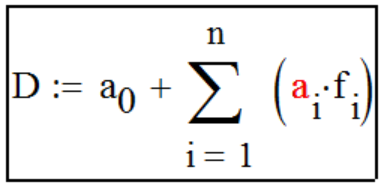
Вид
образующей функции
f[i]
ряда Фурье
f[i] = sin(ω * ti + φ),
где
ω - частота;
ω = 2 * π / Τ
Τ - период;
φ - фаза;
ti - моменты времени
наблюдений;
ti = Δt * i ;
Δt - шаг по времени.
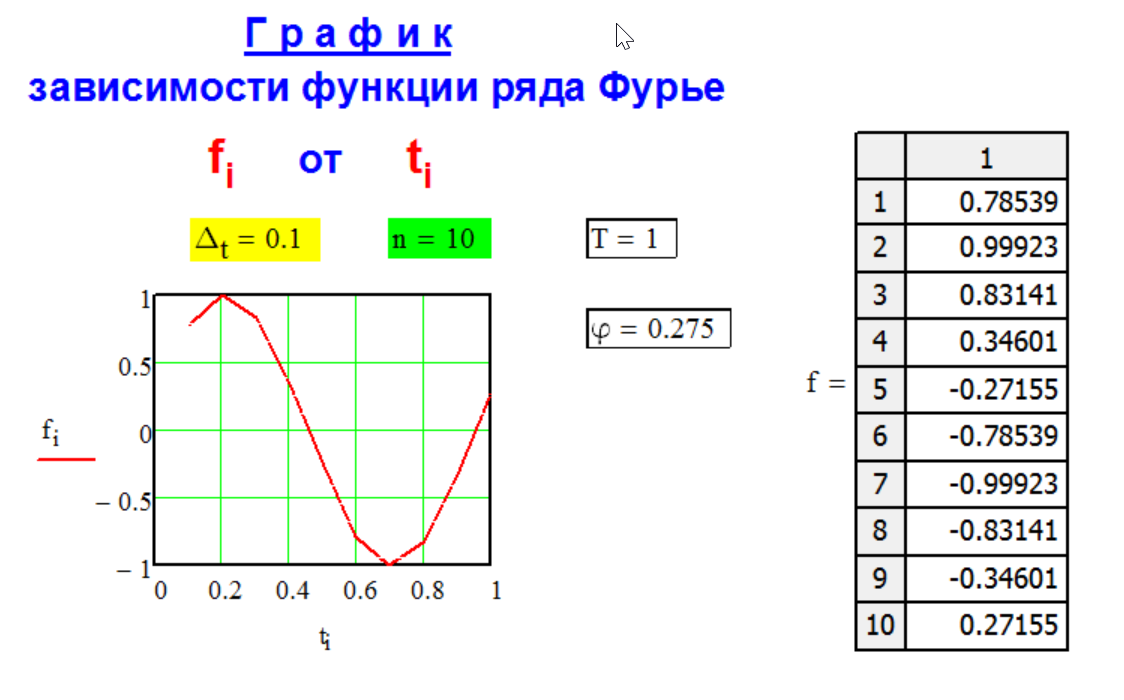


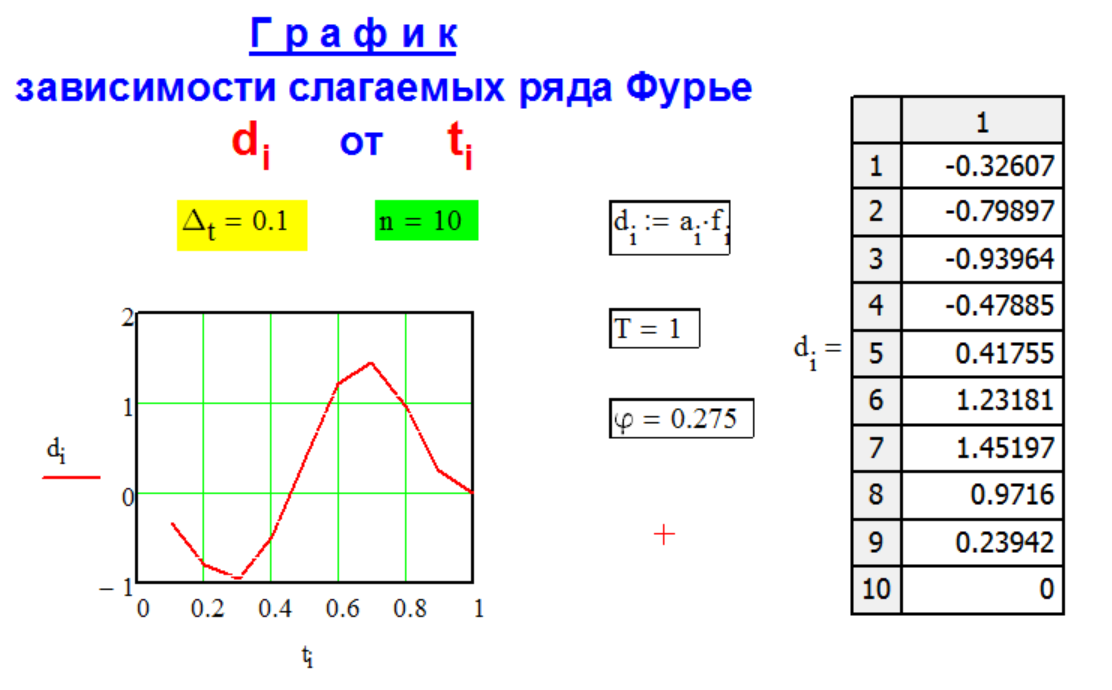
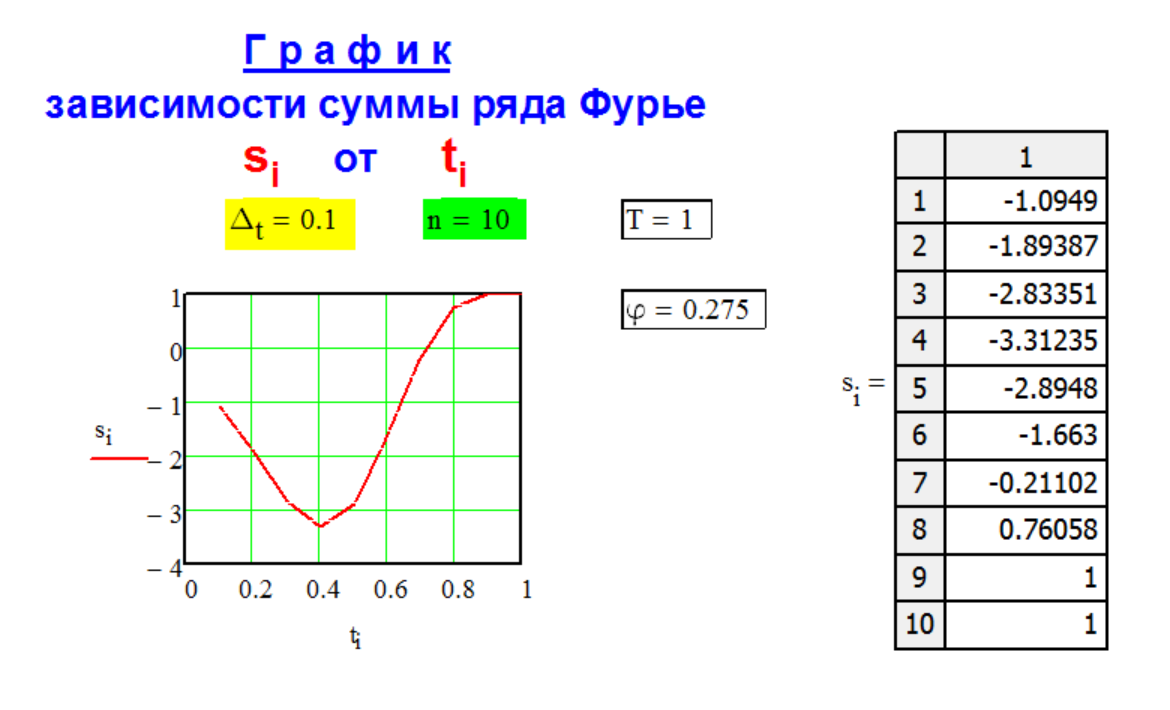
Метод CFG-1-3
декомпозиции
числа
рядом Фурье
со
свободным членом.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
ф у н к ц и и
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
к о э ф ф и ц и е н т о в
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
с у м м ы
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
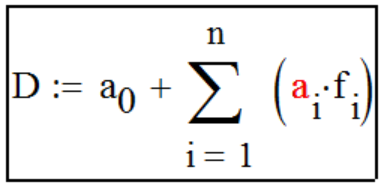
Вид
образующей функции
f[i]
ряда Фурье
f[i] = exp[-(ω * ti + φ)] ,
где
ω - частота;
ω = 2 * π / Τ
Τ - период;
φ - фаза;
ti - моменты времени
наблюдений;
ti = Δt * i ;
Δt - шаг по времени.
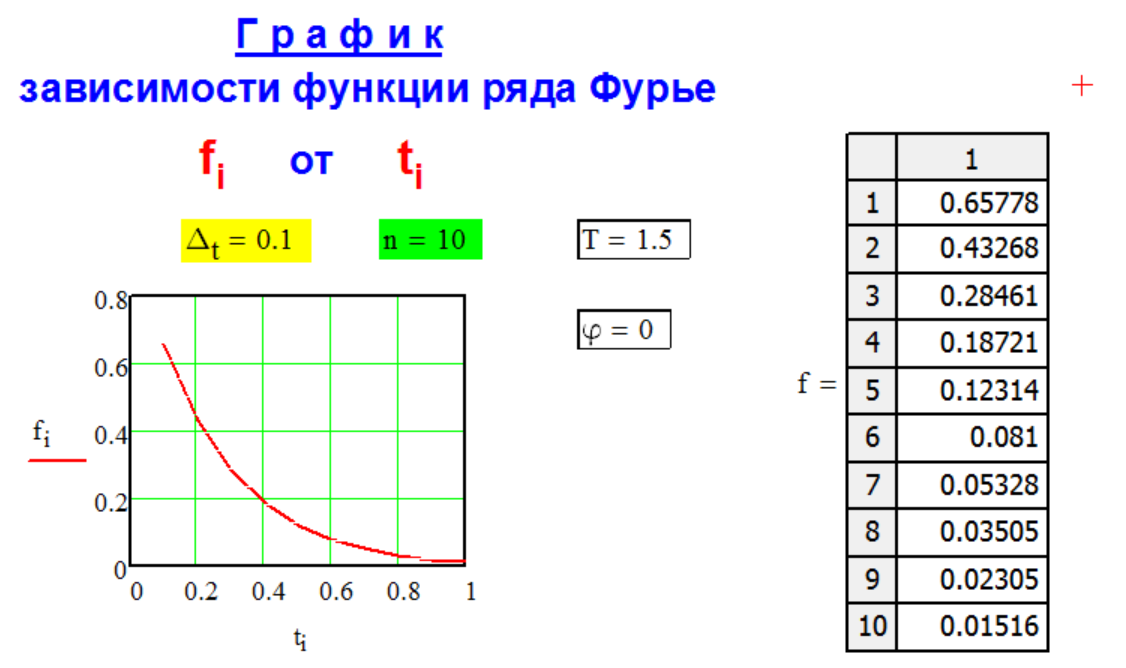


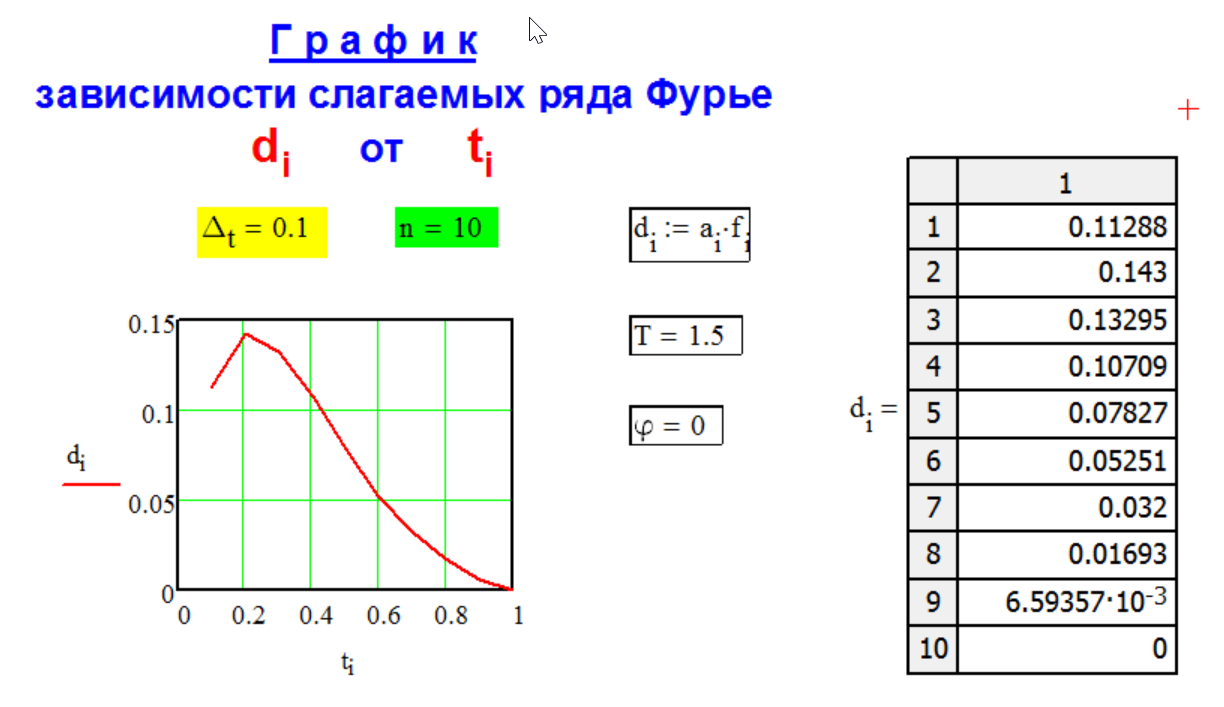
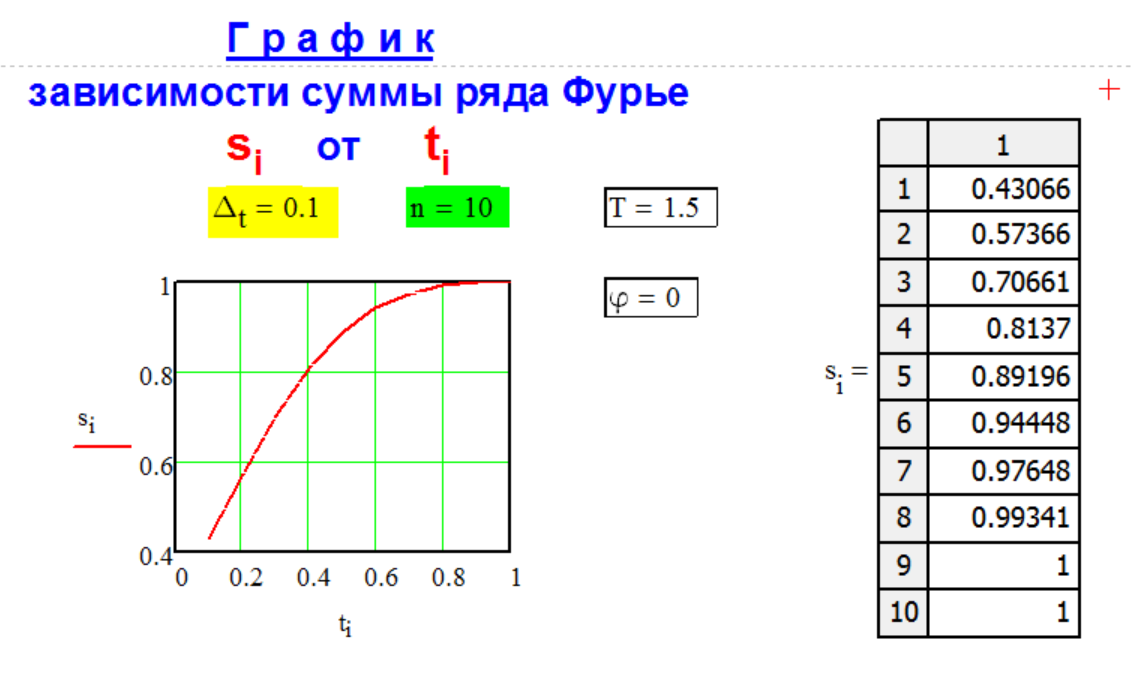
Метод CFG-1-4
декомпозиции
числа
рядом Фурье
со
свободным членом.
РЕЗУЛЬТАТЫ
РАСЧЁТА:
ГРАФИКИ
РАСЧЁТА:
Г Р А Ф И К
ф у н к ц и и
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
к о э ф ф и ц и е н т о в
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
р а с ч ё т н ы х
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
Г Р А Ф И К
с у м м ы
с л а г а е м ы х
р я д а Ф у р ь е.
Расчётные
интервалы времени,
ti .
У Д А Ч И !
П О Б Е Д Ы !
